《2025年课堂精练九年级数学上册北师大版四川专版》

某研究性学习小组在探究矩形的折纸问题时,将一块三角尺的直角顶点绕着矩形 $ABCD (AB ＜ BC)$ 的对角线交点 $O$ 旋转(如图①→②→③),图中 $M$,$N$ 分别为三角尺的直角边与矩形 $ABCD$ 的边 $CD$,$BC$ 的交点.

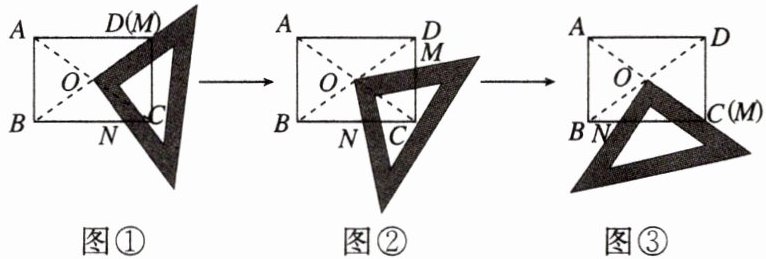
(1)该学习小组中一名成员意外地发现：在图①(三角尺的一直角边与 $OD$ 重合)中,$BN^{2} = CD^{2} + CN^{2}$；在图③(三角尺的一直角边与 $OC$ 重合)中,$CN^{2} = BN^{2} + CD^{2}$. 请你对这名成员在图①和图③中发现的结论选择其一说明理由.
(2)试探究图②中 $BN$,$CN$,$CM$,$DM$ 这四条线段之间的关系,写出你的结论,并说明理由.

答案：
解：
(1)选①.理由如下：
如图①,连接DN.
∵四边形ABCD是矩形，
∴OB=OD.
∵∠DON=90°，
∴BN=DN.
∵∠BCD=90°，
∴DN²=CD²+CN²，
∴BN²=CD²+CN².
　　　　 　　
(2)BN²+DM²=CM²+CN².理由如下：
如图②,延长NO交AD于点P,连接PM,MN.
∵四边形ABCD是矩形,
∴OD=OB,AD//BC，
∴∠DPO=∠BNO,∠PDO=∠NBO.
在△BON和△DOP中，∠NBO=∠PDO，
∠BNO=∠DPO，
OB=OD，
∴△BON≌△DOP(AAS)，
∴ON=OP,BN=DP.
∵∠MON=90°，
∴PM=MN.
∵∠ADC=∠BCD=90°，
∴PM²=PD²+DM²,MN²=CM²+CN²，
∴PD²+DM²=CM²+CN²，
∴BN²+DM²=CM²+CN².

如图,在 $\triangle ABC$ 中,点 $O$ 是边 $AC$ 上一个动点,过点 $O$ 作直线 $EF // BC$ 分别交 $\angle ACB$,$\angle ACD$ 的平分线于点 $E$,$F$.
(1)若 $CE = 8$,$CF = 6$,求 $OC$ 的长.
(2)连接 $AE$,$AF$. 问：当点 $O$ 在边 $AC$ 上运动到什么位置时,四边形 $AECF$ 是矩形？并说明理由.
]

答案： 解：
(1)
∵EF交∠ACB的平分线于点E，交∠ACD的平分线于点F，
∴∠OCE=∠BCE,∠OCF=∠DCF.
∵EF//BC，
∴∠OEC=∠BCE,∠OFC=∠DCF，
∴∠OEC=∠OCE,∠OFC=∠OCF，
∴OE=OC,OF=OC，
∴OE=OF.
∵∠OCE+∠BCE+∠OCF+∠DCF=180°，
∴∠ECF=90°，
在Rt△CEF中，由勾股定理得，EF=√(CE²+CF²)=10,
∴OC=OE=1/2 EF=5.
(2)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下：
当O为AC的中点时,AO=CO.
∵EO=FO，
∴四边形AECF是平行四边形.
∵∠ECF=90°，
∴□AECF是矩形.