《2025年课堂精练九年级数学上册北师大版四川专版》

定义：只含有___个未知数,并且未知数的___次数为___的___方程,叫做一元二次方程。
一般形式：___。
基本解法：___、___、___。
根的判别式：
$ \Delta = b ^ { 2 } - 4 a c \left\{ \begin{array} { l } { \textcircled { 1 } \text { 当 } \Delta $_________$0 \text { 时,方程有两 } } \\ { \text { 个不相等的实数根; } } \\ { \textcircled { 2 } \text { 当 } \Delta $_________$0 \text { 时,方程有两 } } \\ { \text { 个相等的实数根; } } \\ { \textcircled { 3 } \text { 当 } \Delta $_________$0 \text { 时,方程没有 } } \\ { \text { 实数根. } } \end{array} \right. $
求根公式：$$ x = \frac { - b \pm \sqrt { b ^ { 2 } - 4 a c } } { 2 a } ( b ^ { 2 } - 4 a c $$___$$ 0 ) $$。
根与系数的关系：$$ x _ { 1 } + x _ { 2 } = - \frac { b } { a }, x _ { 1 } x _ { 2 } = \frac { c } { a } $$。
一元二次方程的应用：几何问题、实际问题。

答案： 一 最高 2 整式
$ax^{2}+bx+c=0$($a,b,c$为常数,$a≠0$)
配方法 公式法 因式分解法
＞ = ＜
≥

1. 方程$$ x ( x + 2 ) = 0 $$的根是( ).

A. x = 2
B. x = 0
C. x _ { 1 } = 0, x _ { 2 } = - 2
D. x _ { 1 } = 0, x _ { 2 } = 2

答案： C

2. 用配方法解方程$$ x ^ { 2 } - 2 x - 5 = 0 $$时,原方程应变形为( ).

A. ( x + 1 ) ^ { 2 } = 6
B. ( x - 1 ) ^ { 2 } = 6
C. ( x + 2 ) ^ { 2 } = 9
D. ( x - 2 ) ^ { 2 } = 9

答案： B

3. 已知关于 x 的一元二次方程$ m x ^ { 2 } - ( m + 2 ) x + \frac { m } { 4 } = 0 $有两个不相等的实数根 x _ { 1 } , x _ { 2 } ,若$ \frac { 1 } { x _ { 1 } } + \frac { 1 } { x _ { 2 } } = 4 m ,$则 m 的值是( ).

A.2
B.- 1
C.2 或 - 1
D.不存在

答案： A

4. 欧几里得的《几何原本》记载,形如$$ x ^ { 2 } + a x = b ^ { 2 } $$的方程的图解法：如图,画$$ \mathrm { Rt } \triangle A B C $$,使$$ \angle A C B = 90 ^ { \circ } $$,$$ B C = \frac { a } { 2 } $$,$$ A C = b $$,再在斜边$$ A B $上截取$ B D = \frac { a } { 2 } $$,则该方程的一个正根是( ).


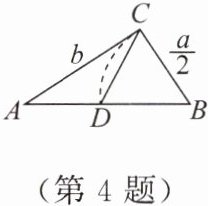
A.$$ A C $$的长
B.$$ A D $$的长
C.$$ B C $$的长
D.$$ C D $$的长

答案： B

5. 已知关于$$ x $的方程$ x ^ { 2 } + 3 x - m = 0 $的一个解为$ - 3 $$,则它的另一个解是___。

答案： 0

6. 关于$$ x $的一元二次方程$ ( m - 5 ) x ^ { 2 } + 2 x + 2 = 0 $$有实根,则$$ m $$的最大整数解是___。

答案： 4

7. 一元二次方程$$ x ^ { 2 } - 4 x + 2 = 0 $的两根为$ x _ { 1 } $$,$$ x _ { 2 } $$,则$$ x _ { 1 } ^ { 2 } - 4 x _ { 1 } + 2 x _ { 1 } x _ { 2 } $$的值为___。

答案： 2