《2025年课堂精练九年级数学上册北师大版四川专版》

9. 如图,将$\triangle PQR沿着PQ的方向平移到\triangle P'Q'R'$的位置,它们重叠部分的面积是$\triangle PQR$面积的一半.若$PQ = \sqrt{2}$,则平移的距离$PP'$是 .

答案： √2-1

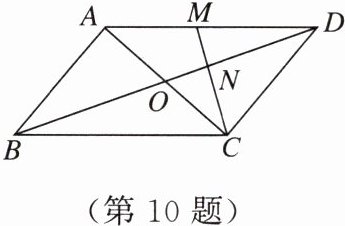
10. 如图,在$□ ABCD$中,对角线$AC$,$BD交于点O$.点$M是AD$的中点,连接$CM交BD于点N$,且$ON = 1$.
(1)求$BD$的长；
(2)若$\triangle DCN的面积为2$,求四边形$ABCD$的面积.

答案： 解:
(1)
∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△MND∽△CNB,
∴MD BC=DN BN.
∵点M是AD的中点,
∴MD=12AD=12BC,即MD BC=12,
∴DN BN=12,即BN=2DN.设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x-1,
∴x+1=2(x-1),解得x=3,
∴BD=2x=6.
(2)
∵△MND∽△CNB,且相似比为1:2,
∴MN:CN=1:2,S△MND:S△CND=1:2.
∵△DCN的面积为2,
∴△MND的面积为1,
∴△MCD的面积为3.
∵S□ABCD=AD⋅h,S△MCD=12MD⋅h=14AD⋅h,
∴S□ABCD=4S△MCD=12.

阅读下面的短文,并解答下列问题：
我们把相似形的概念推广到空间：如果两个几何体的大小不一定相等,但形状完全相同,就把它们叫做相似体.如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比$(a:b)$.
设$S_{甲}$,$S_{乙}$分别表示这两个正方体的表面积,则$\dfrac{S_{甲}}{S_{乙}} = \dfrac{6a^2}{6b^2} = \left(\dfrac{a}{b}\right)^2$.
又设$V_{甲}$,$V_{乙}$分别表示这两个正方体的体积,则$\dfrac{V_{甲}}{V_{乙}} = \dfrac{a^3}{b^3} = \left(\dfrac{a}{b}\right)^3$.
(1)下列几何体中,一定属于相似体的是( ).
A. 两个球体
B. 两个锥体
C. 两个圆柱体
D. 两个长方体
(2)请归纳出相似体的三条主要性质：
①相似体的一切对应线段(或弧)长的比等于 ；
②相似体的表面积的比等于 ；
③相似体的体积的比等于 .
(3)假定在完全正常发育的条件下,不同时期的同一人的人体是相似体,一个小朋友上幼儿园时身高为$1.1\ m$,体重为$18\ kg$,到了九年级时,身高为$1.65\ m$,问他的体重是多少？(不考虑不同时期人体平均密度的变化)

答案： 解:
(1)A
(2)①相似比 ②相似比的平方 ③相似比的立方
(3)由题意知他的体积比为(1.11.65)3.又因为体重之比等于体积比,若设九年级时的体重为x kg,则有(1.11.65)3=18x,解得x=60.75.答:九年级时他的体重为60.75 kg.

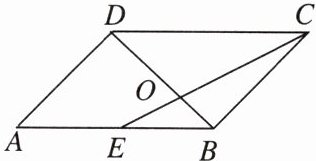
如图,在$□ ABCD$中,点$E是AB$的中点,$CE和BD交于点O$.设$\triangle OCD的面积为m$,$\triangle OEB的面积为\sqrt{5}$,则下列结论正确的是( ).


A.$m = 5$
B.$m = 4\sqrt{5}$
C.$m = 3\sqrt{5}$
D.$m = 10$

答案： B