《2025年名校课堂七年级数学上册湘教版广西专版》

12. 新考向 地域文化(教材 P119 练习 T1 变式)邕江,是南宁市主要的城市用水源,被称为南宁的母亲河.A,B 两地分别位于邕江上下游,相距 280 km,一艘轮船从 A 地到 B 地,顺流航行需要 14 h；从 B 地到 A 地,逆流航行需要 20 h.问轮船在静水中的速度为多少？设该轮船在静水中的速度为 $x$ km/h,水流速度为 $y$ km/h,则可列方程组：$\begin{cases}14(x+y)=280\\20(x-y)=280\end{cases}$.

答案： {14(x+y)=280, 20(x-y)=280

13. 笔记本 5 元/本,钢笔 7 元/支,某同学购买笔记本和钢笔恰好用去 100 元,那么最多购买钢笔10支.

答案： 10

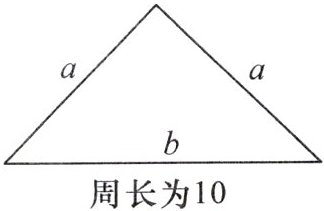
14. 清华附中校本经典题一个三角形的三边长和周长如图所示.
(1)请列出关于未知数 $a,b$ 的方程.
(2)若 $a = 3$,求 $b$ 的值.
]

答案： 解：
(1)由题意可得，2a+b=10.
(2)把a=3代入2a+b=10，得6+b=10，解得b=4.

15. 石家庄外国语校本经典题某两位数,两个数位上的数字之和为 11.这个两位数加上 45,得到的新两位数恰好等于原两位数的两个数字交换位置所表示的数,求原两位数.
(1)列一元一次方程求解；
(2)设原两位数的十位数字为 $x$,个位数字为 $y$,列二元一次方程组；
(3)检验(1)中求得的结果是否满足(2)中的方程组.

答案： $(1)$ 列一元一次方程求解
解：设原两位数的十位数字为$x$，则个位数字为$11 - x$。
原两位数为$10x+(11 - x)$，交换位置后的新两位数为$10(11 - x)+x$。
根据题意可列方程：
$\begin{aligned}10x+(11 - x)+45&=10(11 - x)+x\\10x + 11 - x + 45&=110 - 10x + x\\9x+56&=110 - 9x\\9x + 9x&=110 - 56\\18x&=54\\x&=3\end{aligned}$
个位数字为$11 - 3 = 8$，所以原两位数是$38$。
$(2)$ 列二元一次方程组
设原两位数的十位数字为$x$，个位数字为$y$。
因为两个数位上的数字之和为$11$，所以$x + y=11$；
原两位数为$10x + y$，交换位置后的新两位数为$10y + x$，又因为这个两位数加上$45$等于新两位数，所以$10x + y+45 = 10y + x$。
则方程组为$\begin{cases}x + y = 11\\10x + y+45 = 10y + x\end{cases}$。
$(3)$ 检验结果
把$x = 3$，$y = 8$代入方程组$\begin{cases}x + y = 11\\10x + y+45 = 10y + x\end{cases}$。
对于方程$x + y = 11$：左边$=3 + 8=11$，右边$=11$，左边$=$右边。
对于方程$10x + y+45 = 10y + x$：
左边$=10×3 + 8+45=30 + 8+45 = 83$，
右边$=10×8 + 3=80 + 3 = 83$，左边$=$右边。
所以$(1)$中求得的结果$x = 3$，$y = 8$满足$(2)$中的方程组。
综上，答案依次为：$(1)$原两位数是$38$；$(2)$$\begin{cases}x + y = 11\\10x + y+45 = 10y + x\end{cases}$；$(3)$满足。

1. (2023·贵港覃塘区期末)若$\left\{\begin{array}{l} x= 3,\\ y= -1\end{array} \right. $是关于x,y的二元一次方程$3x-ay= 8$的一组解,则a的值是-1.

答案： -1

2. 已知$\left\{\begin{array}{l} x= 2,\\ y= m\end{array} \right. 是方程3x+2y= 10$的一个解,则m的值是2.

答案： 2

3. 已知$\left\{\begin{array}{l} x= 3,\\ y= 2\end{array} \right. $是关于x,y的二元一次方程$ax-by= 1$的一组解,则$6a-4b+2025= $2027.

答案： 2027

4. (2024·贵港港南区期中)如果方程组$\left\{\begin{array}{l} x+y= ★,\\ 2x+y= 16\end{array} \right. 的解为\left\{\begin{array}{l} x= 6,\\ y= ■,\end{array} ■, \right. $那么被“★”“■”遮住的两个数分别为 (C)
A.3,10
B.4,10
C.10,4
D.10,3

答案： C