第111页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 如图,用圆规比较两条线段$A'B'和AB$的长短,则$A'B'$
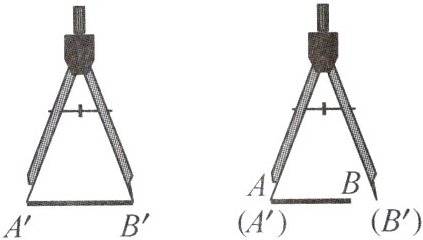
>
$AB$.(填“$>$”“$=$”或“$<$”)
答案:
>
2. 如图所示,则:

(1)$AC= BC+$
(2)$CD= AD-$
(3)$CD= $
(4)$AB+BC= $

(1)$AC= BC+$
AB
;(2)$CD= AD-$
AC
;(3)$CD= $
BD
$-BC$;(4)$AB+BC= $
AD
$-CD$.
答案:
(1)AB
(2)AC
(3)BD
(4)AD
(1)AB
(2)AC
(3)BD
(4)AD
3. 新考向 真实情境 贵岑高速是目前贵港通往云浮最便捷、行车距离最短的一条高速公路.在修建该高速公路时尽量将弯曲的道路改直以缩短行程,其道理可以用数学知识解释为
两点之间,线段最短
.
答案:
两点之间,线段最短
4. 杭州外国语校本经典题 下面四种说法中,正确的是(
A.两点间的连线的长度,叫作两点间的距离
B.连接两点的线段,叫作两点间的距离
C.两点间的距离就是两点间的路程
D.两点间的距离是连接两点的线段的长度
D
)A.两点间的连线的长度,叫作两点间的距离
B.连接两点的线段,叫作两点间的距离
C.两点间的距离就是两点间的路程
D.两点间的距离是连接两点的线段的长度
答案:
D
5. 已知:如图,线段$a$,$b$.
求作:线段$AB$,使得$AB= a+b$.
小明给出了四个步骤:①在射线$AM上画线段AP= a$;②则线段$AB= a+b$;③在射线$PM上画线段PB= b$;④画射线$AM$.正确的顺序是(
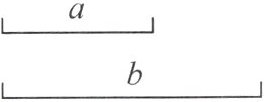
A.①②③④
B.④①③②
C.④③①②
D.④②①③
求作:线段$AB$,使得$AB= a+b$.
小明给出了四个步骤:①在射线$AM上画线段AP= a$;②则线段$AB= a+b$;③在射线$PM上画线段PB= b$;④画射线$AM$.正确的顺序是(
B
)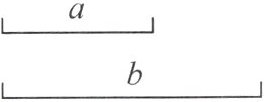
A.①②③④
B.④①③②
C.④③①②
D.④②①③
答案:
B
6. (2024·贵港平南县期末)如图,已知线段$a$,$b$,请用尺规作线段$MN= 2a-b$.(不写作法,保留作图痕迹)
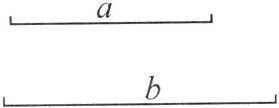
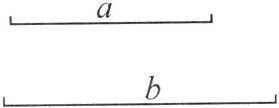
答案:
解:如图,线段MN即为所求.

解:如图,线段MN即为所求.

7. 若点$C在线段AB$上,不能说明$C是线段AB$的中点的是(
A.$AB= 2AC$
B.$CB= \frac{1}{2}AB$
C.$AC= CB$
D.$AC+CB= AB$
D
)A.$AB= 2AC$
B.$CB= \frac{1}{2}AB$
C.$AC= CB$
D.$AC+CB= AB$
答案:
D
8. 如图,$AB= 8\mathrm{cm}$,$C是线段AB上靠近点B$的四等分点,$M是线段AC$的中点,则$MC$的长是(

A.$2\mathrm{cm}$
B.$3\mathrm{cm}$
C.$4\mathrm{cm}$
D.$6\mathrm{cm}$
B
)
A.$2\mathrm{cm}$
B.$3\mathrm{cm}$
C.$4\mathrm{cm}$
D.$6\mathrm{cm}$
答案:
B
9. (2024·贵港平南县期末改编)补全解题过程.
如图,已知点$C在线段AB$上,$AB= 18$,$BC= \frac{1}{3}AB$,$D是线段AB$的中点,求线段$CD$的长.

解:因为$AB= 18$,$BC= \frac{1}{3}AB$,
所以$BC= \frac{1}{3}×$
因为$D是线段AB$的中点,
所以$BD= \frac{1}{2}AB= \frac{1}{2}×$
所以$CD= BD-$
如图,已知点$C在线段AB$上,$AB= 18$,$BC= \frac{1}{3}AB$,$D是线段AB$的中点,求线段$CD$的长.

解:因为$AB= 18$,$BC= \frac{1}{3}AB$,
所以$BC= \frac{1}{3}×$
18
=6
.因为$D是线段AB$的中点,
所以$BD= \frac{1}{2}AB= \frac{1}{2}×$
18
=9
(依据:线段中点的定义
).所以$CD= BD-$
BC
=9
-6
=3
.
答案:
18 6 18 9 线段中点的定义 BC 9 6 3
10. (2023·南宁月考)已知线段$AB= 5\mathrm{cm}$,在直线$AB上画线段BC= 2\mathrm{cm}$,则$AC$的长是(
A.$3\mathrm{cm}$
B.$7\mathrm{cm}$
C.$3\mathrm{cm}或7\mathrm{cm}$
D.无法确定
C
)A.$3\mathrm{cm}$
B.$7\mathrm{cm}$
C.$3\mathrm{cm}或7\mathrm{cm}$
D.无法确定
答案:
C
查看更多完整答案,请扫码查看


