第21页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
10. 数学活动中,王老师给同学们出了一道题:规定一种新运算“★”,对于任意有理数$a和b$,有$a★b = a - b + 1$.请根据新运算,计算$(2★3)★2$的值是(
A.0
B.$-1$
C.$-2$
D.1
B
)A.0
B.$-1$
C.$-2$
D.1
答案:
B
11. (2023·柳州鹿寨县期末)某公交车上原有22人,经过3个站点时上、下车情况如下(上车记为正,下车记为负):$(+3,-7)$,$(+6,-4)$,$(+2,-1)$,则经过3个站点后车上还有
21
人.
答案:
21
12. 南京师大附中校本经典题 如图,输入$-1$,按程序运算(完成一个方框内的运算后,把结果输入下一个方框继续进行运算),则输出的结果为
]

5
.]

答案:
5
13. 计算:
(1) $(-9\dfrac{1}{3})-\vert -4\dfrac{5}{6}\vert +\vert 0-5\dfrac{1}{6}\vert -\dfrac{2}{3}$;
(2) $6\dfrac{3}{7}+24-18+4\dfrac{4}{7}-16+18-6.8-3\dfrac{1}{5}$.
(1) $(-9\dfrac{1}{3})-\vert -4\dfrac{5}{6}\vert +\vert 0-5\dfrac{1}{6}\vert -\dfrac{2}{3}$;
(2) $6\dfrac{3}{7}+24-18+4\dfrac{4}{7}-16+18-6.8-3\dfrac{1}{5}$.
答案:
解:
(1)原式=$-9\frac{1}{3}-4\frac{5}{6}+5\frac{1}{6}-\frac{2}{3}=(-9\frac{1}{3}-\frac{2}{3})+(-4\frac{5}{6}$$+5\frac{1}{6})=-10+\frac{1}{3}=-9\frac{2}{3}$.
(2)原式=$(6\frac{3}{7}+4\frac{4}{7})+(-18+18)+(-6.8-3.2)+24-16=11+0-10+24-16=9$.
(1)原式=$-9\frac{1}{3}-4\frac{5}{6}+5\frac{1}{6}-\frac{2}{3}=(-9\frac{1}{3}-\frac{2}{3})+(-4\frac{5}{6}$$+5\frac{1}{6})=-10+\frac{1}{3}=-9\frac{2}{3}$.
(2)原式=$(6\frac{3}{7}+4\frac{4}{7})+(-18+18)+(-6.8-3.2)+24-16=11+0-10+24-16=9$.
14. 新考向 真实情境 (2024·南宁期中)如图为南宁市地铁1号线路线图的一部分,小明想乘坐地铁参加社会实践活动,他从南湖站出发,终点站为A站.如果规定往广西大学的方向为正,往埌东客运站的方向为负,当天的行程站数按先后顺序依次记录如下:$+5,-3,+7,-8,+9,-2,-7,+2$.
(1) A站是哪一站?
(2) 若相邻两站之间的平均距离约为$1.2 km$,则小明这次乘坐地铁参加社会实践活动的总路程约是多少千米?
]
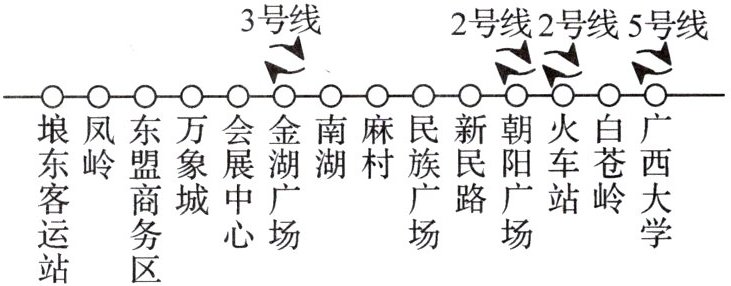
(1) A站是哪一站?
(2) 若相邻两站之间的平均距离约为$1.2 km$,则小明这次乘坐地铁参加社会实践活动的总路程约是多少千米?
]

答案:
解:
(1)由题意,得5-3+7-8+9-2-7+2=3,所以 A 站是新民路.
(2)$|+5|+|-3|+|+7|+|-8|+|+9|+|-2|+|-7|+|+2|=$5+3+7+8+9+2+7+2=43,所以 43×1.2=51.6(km). 答:小明这次乘坐地铁参加社会实践活动的总路程约是51.6 km.
(1)由题意,得5-3+7-8+9-2-7+2=3,所以 A 站是新民路.
(2)$|+5|+|-3|+|+7|+|-8|+|+9|+|-2|+|-7|+|+2|=$5+3+7+8+9+2+7+2=43,所以 43×1.2=51.6(km). 答:小明这次乘坐地铁参加社会实践活动的总路程约是51.6 km.
15. (2024·广西大学附中月考)【信息提取】在有些情况下,不需要计算出结果也能把绝对值符号去掉.如:$\vert 6 + 7\vert = 6 + 7$,$\vert 6 - 7\vert = 7 - 6$,$\vert 7 - 6\vert = 7 - 6$,$\vert -6 - 7\vert = 6 + 7$.
【初步体验】
(1) 根据上面的规律,把下列各式写成去掉绝对值符号的形式(不要求计算出结果):
① $\vert 7 - 21\vert =$
② $\vert \dfrac{7}{17}-\dfrac{7}{18}\vert =$
【拓广应用】
(2) 计算:$\vert \dfrac{1}{3}-\dfrac{1}{2}\vert +\vert \dfrac{1}{4}-\dfrac{1}{3}\vert +\vert \dfrac{1}{5}-\dfrac{1}{4}\vert +… +\vert \dfrac{1}{2025}-\dfrac{1}{2024}\vert +\vert \dfrac{1}{2026}-\dfrac{1}{2025}\vert$.
【初步体验】
(1) 根据上面的规律,把下列各式写成去掉绝对值符号的形式(不要求计算出结果):
① $\vert 7 - 21\vert =$
21-7
;② $\vert \dfrac{7}{17}-\dfrac{7}{18}\vert =$
$\frac{7}{17}-\frac{7}{18}$
.【拓广应用】
(2) 计算:$\vert \dfrac{1}{3}-\dfrac{1}{2}\vert +\vert \dfrac{1}{4}-\dfrac{1}{3}\vert +\vert \dfrac{1}{5}-\dfrac{1}{4}\vert +… +\vert \dfrac{1}{2025}-\dfrac{1}{2024}\vert +\vert \dfrac{1}{2026}-\dfrac{1}{2025}\vert$.
解:原式=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\cdots+\frac{1}{2024}-\frac{1}{2025}+\frac{1}{2025}-\frac{1}{2026}=\frac{1}{2}-\frac{1}{2026}=\frac{1012}{2026}=\frac{506}{1013}$.
答案:
解:
(1)①21-7 ②$\frac{7}{17}-\frac{7}{18}$
(2)原式=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\cdots+\frac{1}{2024}-\frac{1}{2025}+\frac{1}{2025}-\frac{1}{2026}=\frac{1}{2}-\frac{1}{2026}=\frac{1012}{2026}=\frac{506}{1013}$.
(1)①21-7 ②$\frac{7}{17}-\frac{7}{18}$
(2)原式=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\cdots+\frac{1}{2024}-\frac{1}{2025}+\frac{1}{2025}-\frac{1}{2026}=\frac{1}{2}-\frac{1}{2026}=\frac{1012}{2026}=\frac{506}{1013}$.
查看更多完整答案,请扫码查看


