第104页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
10. (2024·南宁北附实验学校月考)如图所示的是某月的月历表,在此月历表上可以用一个“十”字圈出5个阿拉伯数字(如3,9,10,11,17).照此方法,若圈出的5个数的和为115,则这5个数中的最大数为
]

30
.]

答案:
30
11. (2024·贵港桂平市期末)为了丰富同学们的课余生活、拓展同学们的视野,学校书店准备购进甲、乙两类中学生书刊,已知甲类书刊比乙类书刊每本贵2元,购买500本甲类书刊和400本乙类书刊共需要8200元,其中甲、乙两类书刊的进价和售价如下表:
|书刊种类|甲|乙|
|进价/(元·本⁻^1)|$x$|$y$|
|售价/(元·本⁻^1)|20|13|

(1)求$x$,$y$的值;
(2)第二次学校书店购进了1000本甲类书刊和500本乙类书刊,为了扩大销量,书店准备对甲类书刊进行打折出售,乙类书刊价格不变,全部售完后总利润为8500元,求甲类书刊打了几折.
|书刊种类|甲|乙|
|进价/(元·本⁻^1)|$x$|$y$|
|售价/(元·本⁻^1)|20|13|

(1)求$x$,$y$的值;
(2)第二次学校书店购进了1000本甲类书刊和500本乙类书刊,为了扩大销量,书店准备对甲类书刊进行打折出售,乙类书刊价格不变,全部售完后总利润为8500元,求甲类书刊打了几折.
答案:
解:
(1)由题意,得{x-y=2,500x+400y=8200,解得{x=10,y=8.
(2)设甲类书刊打了m折.由题意,得1000×20×0.1m+500×13-(1000×10+500×8)=8500,解得m=8.答:甲类书刊打了八折.
(1)由题意,得{x-y=2,500x+400y=8200,解得{x=10,y=8.
(2)设甲类书刊打了m折.由题意,得1000×20×0.1m+500×13-(1000×10+500×8)=8500,解得m=8.答:甲类书刊打了八折.
12. 新考向 跨学科 华氏温度$F(^{\circ}F)与摄氏温度T(^{\circ}C)之间的转换关系是F = 32 + 1.8T$.下列温度中,与华氏温度$212^{\circ}F$接近的是 (
A.水沸腾的温度
B.人体的温度
C.舒适的室温
D.水结冰时的温度
A
)A.水沸腾的温度
B.人体的温度
C.舒适的室温
D.水结冰时的温度
答案:
A
13. (2024·南宁外国语学校月考)综合与实践:如图1所示的是一架自制天平,支点$O$固定不变,右侧托盘固定在点$B$处,左侧托盘的点$P可以在横梁AC$段滑动.已知$OB = OC = 15\ cm$,$AO = 50\ cm$,1个$M$物体和1个$N物体的质量分别为m\ g$,$n\ g$,已知天平平衡时,左盘物体质量$×OP = 右盘物体质量×OB$.(不计托盘与横梁质量)
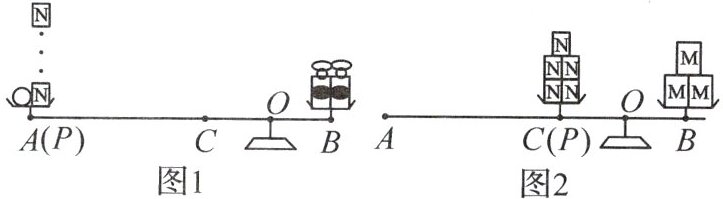
(1)若左侧托盘固定在点$C$处,如图2所示天平平衡,$m = 5$,则$n = $
(2)若右侧托盘放置1个$100\ g$的砝码,左侧托盘放9个$M$物体和30个$N$物体,滑动点$P到PC = 5\ cm$时,天平平衡,已知$m$,$n$为整数,求$m + n$的值;
(3)测量小球的质量:如图1,右侧托盘放置2个$100\ g$砝码,左侧托盘放入一个小球和若干个$N$物体,滑动点$P至点A$处,天平恰好平衡,若再次向左侧托盘中加入相同数量的$N$物体,发现点$P移动到PC = OC$时,天平平衡,求这个小球的质量.

(1)若左侧托盘固定在点$C$处,如图2所示天平平衡,$m = 5$,则$n = $
3
;(2)若右侧托盘放置1个$100\ g$的砝码,左侧托盘放9个$M$物体和30个$N$物体,滑动点$P到PC = 5\ cm$时,天平平衡,已知$m$,$n$为整数,求$m + n$的值;
(3)测量小球的质量:如图1,右侧托盘放置2个$100\ g$砝码,左侧托盘放入一个小球和若干个$N$物体,滑动点$P至点A$处,天平恰好平衡,若再次向左侧托盘中加入相同数量的$N$物体,发现点$P移动到PC = OC$时,天平平衡,求这个小球的质量.
答案:
解:
(1)3
(2)根据题意,得(15+5)×(9m+30n)=100×15,整理,得3m+10n=25.因为m,n为整数,所以m=5,n=1.所以m+n=6.
(3)设这个小球的质量为xg,若干个N物体的质量为yg.由题意,得{50(x+y)=2×100×15,30(x+2y)=2×100×15,整理,得{x+y=60,x+2y=100,解得{x=20,y=40.答:这个小球的质量为20g.
(1)3
(2)根据题意,得(15+5)×(9m+30n)=100×15,整理,得3m+10n=25.因为m,n为整数,所以m=5,n=1.所以m+n=6.
(3)设这个小球的质量为xg,若干个N物体的质量为yg.由题意,得{50(x+y)=2×100×15,30(x+2y)=2×100×15,整理,得{x+y=60,x+2y=100,解得{x=20,y=40.答:这个小球的质量为20g.
查看更多完整答案,请扫码查看


