第14页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 填表:
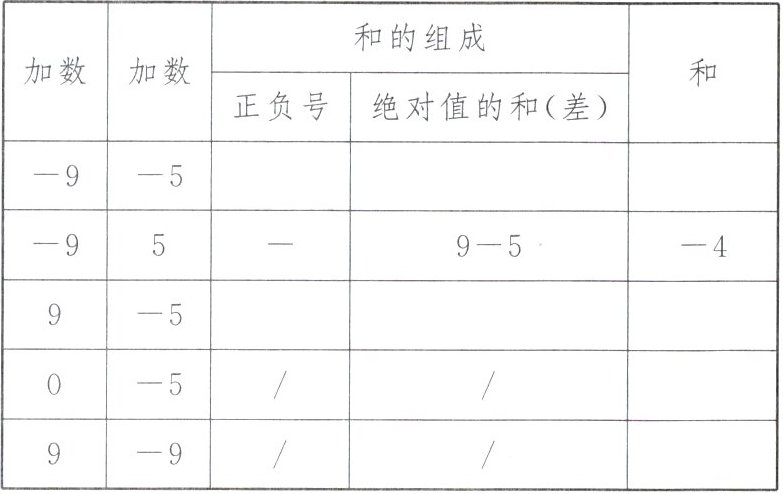
|加数|加数|和的组成|和|
| | |正负号|绝对值的和(差)| |
|$-9$|$-5$|$-$|$9 + 5$|$-14$|
|$-9$|$5$|$-$|$9 - 5$|$-4$|
|$9$|$-5$|$+$|$9 - 5$|$4$|
|$0$|$-5$|$/$|$/$|$-5$|
|$9$|$-9$|$/$|$/$|$0$|

|加数|加数|和的组成|和|
| | |正负号|绝对值的和(差)| |
|$-9$|$-5$|$-$|$9 + 5$|$-14$|
|$-9$|$5$|$-$|$9 - 5$|$-4$|
|$9$|$-5$|$+$|$9 - 5$|$4$|
|$0$|$-5$|$/$|$/$|$-5$|
|$9$|$-9$|$/$|$/$|$0$|
答案:
1. 对于$-9$和$-5$:
根据有理数加法法则,同号两数相加,取相同的符号,并把绝对值相加。
正负号为“$-$”,绝对值的和为$\vert - 9\vert+\vert - 5\vert=9 + 5$,和为$-(9 + 5)=-14$。
2. 对于$9$和$-5$:
根据有理数加法法则,异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值。
因为$\vert9\vert\gt\vert - 5\vert$,正负号为“$+$”,绝对值的差为$9−5$,和为$9+( - 5)=4$。
3. 对于$0$和$-5$:
根据有理数加法法则,$0$加任何数都等于这个数本身,所以和为$-5$。
4. 对于$9$和$-9$:
根据有理数加法法则,互为相反数的两个数相加得$0$,所以和为$0$。
故填表如下:
|加数|加数|和的组成|和|
| | |正负号|绝对值的和(差)| |
|$-9$|$-5$|$-$|$9 + 5$|$-14$|
|$-9$|$5$|$-$|$9 - 5$|$-4$|
|$9$|$-5$|$+$|$9 - 5$|$4$|
|$0$|$-5$|$/$|$/$|$-5$|
|$9$|$-9$|$/$|$/$|$0$|
根据有理数加法法则,同号两数相加,取相同的符号,并把绝对值相加。
正负号为“$-$”,绝对值的和为$\vert - 9\vert+\vert - 5\vert=9 + 5$,和为$-(9 + 5)=-14$。
2. 对于$9$和$-5$:
根据有理数加法法则,异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值。
因为$\vert9\vert\gt\vert - 5\vert$,正负号为“$+$”,绝对值的差为$9−5$,和为$9+( - 5)=4$。
3. 对于$0$和$-5$:
根据有理数加法法则,$0$加任何数都等于这个数本身,所以和为$-5$。
4. 对于$9$和$-9$:
根据有理数加法法则,互为相反数的两个数相加得$0$,所以和为$0$。
故填表如下:
|加数|加数|和的组成|和|
| | |正负号|绝对值的和(差)| |
|$-9$|$-5$|$-$|$9 + 5$|$-14$|
|$-9$|$5$|$-$|$9 - 5$|$-4$|
|$9$|$-5$|$+$|$9 - 5$|$4$|
|$0$|$-5$|$/$|$/$|$-5$|
|$9$|$-9$|$/$|$/$|$0$|
2. (2024·广东)计算$-5 + 3$的结果是 (
A.$-2$
B.$-8$
C.$2$
D.$8$
A
)A.$-2$
B.$-8$
C.$2$
D.$8$
答案:
A
3. (2023·温州)如图,比数轴上点$A表示的数大3$的数是 (

A.$-1$
B.$0$
C.$1$
D.$2$
D
)
A.$-1$
B.$0$
C.$1$
D.$2$
答案:
D
4. 下列运算正确的是 (
A.$(-2)+(-2)= 0$
B.$-6+(+4)= -10$
C.$0+(-3)= 3$
D.$5+(-2)= 3$
D
)A.$(-2)+(-2)= 0$
B.$-6+(+4)= -10$
C.$0+(-3)= 3$
D.$5+(-2)= 3$
答案:
D
5. 若两个有理数的和为$0$,则这两个数 (
A.都是$0$
B.至少有一个是$0$
C.一个是正数,一个是负数
D.互为相反数
D
)A.都是$0$
B.至少有一个是$0$
C.一个是正数,一个是负数
D.互为相反数
答案:
D
6. 新考向 数学文化 (2024·柳州期中)中国人最早使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示方法,图 1 可列式计算为$(+1)+(-1)= 0$,由此可推算图 2 计算所得的结果为 (
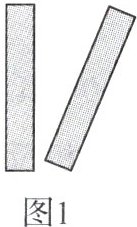
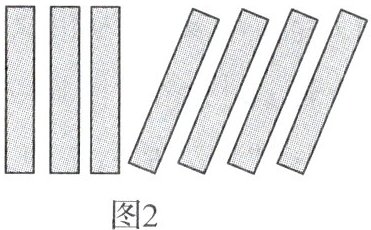
A.$+1$
B.$+7$
C.$-1$
D.$-7$
C
)

A.$+1$
B.$+7$
C.$-1$
D.$-7$
答案:
C
7. 计算:
(1)$(-5.8)+(-4.3)$;(2)$7+(-12)$;
(3)$(-8\frac{2}{3})+0$; (4)$(-6.25)+6\frac{1}{4}$;
(5)$(-0.8)+1.52$; (6)$(-\frac{5}{18})+\frac{1}{6}$.
(1)$(-5.8)+(-4.3)$;(2)$7+(-12)$;
(3)$(-8\frac{2}{3})+0$; (4)$(-6.25)+6\frac{1}{4}$;
(5)$(-0.8)+1.52$; (6)$(-\frac{5}{18})+\frac{1}{6}$.
答案:
解:
(1)原式=-(5.8+4.3)=-10.1.
(2)原式=-(12-7)=-5.
(3)原式$=-8\frac{2}{3}.(4)$原式=0.
(5)原式=0.72.
(6)原式$=-\frac{1}{9}$
(1)原式=-(5.8+4.3)=-10.1.
(2)原式=-(12-7)=-5.
(3)原式$=-8\frac{2}{3}.(4)$原式=0.
(5)原式=0.72.
(6)原式$=-\frac{1}{9}$
8. (2023·南宁江南区期中)气温由$-2\ ^{\circ}C上升3\ ^{\circ}C$后是 (
A.$-5\ ^{\circ}C$
B.$1\ ^{\circ}C$
C.$5\ ^{\circ}C$
D.$3\ ^{\circ}C$
B
)A.$-5\ ^{\circ}C$
B.$1\ ^{\circ}C$
C.$5\ ^{\circ}C$
D.$3\ ^{\circ}C$
答案:
B
9. 一艘潜水艇的高度是$-50$米,一条鲨鱼在潜水艇的正上方$10$米处,这条鲨鱼所在的高度是 (
A.$+10$米
B.$-10$米
C.$-40$米
D.$+40$米
C
)A.$+10$米
B.$-10$米
C.$-40$米
D.$+40$米
答案:
C
查看更多完整答案,请扫码查看


