第34页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 把$(-2)×(-2)×(-2)×(-2)$写成幂式是
$(-2)^{4}$
.
答案:
$(-2)^{4}$
2. 填表:
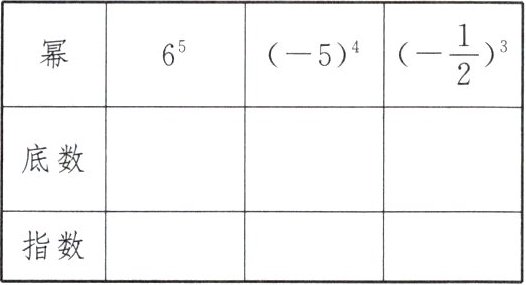

6 -5 $-\frac{1}{2}$ 5 4 3
答案:
6 -5 $-\frac{1}{2}$ 5 4 3
3. $-3^{4}$表示( )
A.$-3乘4$
B.$4个-3$相加
C.$-3的4$次方
D.$3的4$次方的相反
A.$-3乘4$
B.$4个-3$相加
C.$-3的4$次方
D.$3的4$次方的相反
答案:
D
4. $2^{3}$的值等于( )
A.$-6$
B.$6$
C.$8$
D.$-8$
A.$-6$
B.$6$
C.$8$
D.$-8$
答案:
C
5. 计算:$0^{5}= $
0
.
答案:
0
6. 计算:
(1)$0.5^{3}= $
(3)$(-\frac{1}{4})^{3}= $
(1)$0.5^{3}= $
0.125
;(2)$(-3)^{4}= $81
(3)$(-\frac{1}{4})^{3}= $
$-\frac{1}{64}$
;(4)$-1^{2026}= $-1
答案:
(1)0.125
(2)81
(3)$-\frac{1}{64}$
(4)-1
(1)0.125
(2)81
(3)$-\frac{1}{64}$
(4)-1
7. 直接判断下列各式计算结果的符号:
(1)$(-2)^{3}×(-3)^{4}$;
(2)$-6^{2}×(-$1/3)³
(1)$(-2)^{3}×(-3)^{4}$;
(2)$-6^{2}×(-$1/3)³
答案:
1. 对于$(-2)^{3}×(-3)^{4}$:
根据幂的运算法则$a^{n}$($n$为正整数),当$n$为奇数时,$(-a)^{n}=-a^{n}$;当$n$为偶数时,$(-a)^{n}=a^{n}$。
对于$(-2)^{3}$,因为$n = 3$(奇数),所以$(-2)^{3}=-2^{3}=-8$;对于$(-3)^{4}$,因为$n = 4$(偶数),所以$(-3)^{4}=3^{4}=81$。
则$(-2)^{3}×(-3)^{4}=-8×81$,根据有理数乘法法则:两数相乘,异号得负,所以$(-2)^{3}×(-3)^{4}$的结果符号为“$-$”。
2. 对于$-6^{2}×(-\frac{1}{3})^{3}$:
先计算$-6^{2}$,根据运算顺序,$-6^{2}=-(6×6)= - 36$;再计算$(-\frac{1}{3})^{3}$,因为$n = 3$(奇数),所以$(-\frac{1}{3})^{3}=-\frac{1}{27}$。
则$-6^{2}×(-\frac{1}{3})^{3}=-36×(-\frac{1}{27})$,根据有理数乘法法则:两数相乘,同号得正,所以$-6^{2}×(-\frac{1}{3})^{3}$的结果符号为“$+$”。
综上,(1)结果符号为“$-$”;(2)结果符号为“$+$”。
根据幂的运算法则$a^{n}$($n$为正整数),当$n$为奇数时,$(-a)^{n}=-a^{n}$;当$n$为偶数时,$(-a)^{n}=a^{n}$。
对于$(-2)^{3}$,因为$n = 3$(奇数),所以$(-2)^{3}=-2^{3}=-8$;对于$(-3)^{4}$,因为$n = 4$(偶数),所以$(-3)^{4}=3^{4}=81$。
则$(-2)^{3}×(-3)^{4}=-8×81$,根据有理数乘法法则:两数相乘,异号得负,所以$(-2)^{3}×(-3)^{4}$的结果符号为“$-$”。
2. 对于$-6^{2}×(-\frac{1}{3})^{3}$:
先计算$-6^{2}$,根据运算顺序,$-6^{2}=-(6×6)= - 36$;再计算$(-\frac{1}{3})^{3}$,因为$n = 3$(奇数),所以$(-\frac{1}{3})^{3}=-\frac{1}{27}$。
则$-6^{2}×(-\frac{1}{3})^{3}=-36×(-\frac{1}{27})$,根据有理数乘法法则:两数相乘,同号得正,所以$-6^{2}×(-\frac{1}{3})^{3}$的结果符号为“$+$”。
综上,(1)结果符号为“$-$”;(2)结果符号为“$+$”。
8.(2024·贵港覃塘区期中)下列各对数中为相反数的是( )
A.$\frac{2^{2}}{3}与(\frac{2}{3})^{2}$
B.$-2^{2}与(-2)^{2}$
C.$-(+3)与-|-3|$
D.$(-2)^{3}与-2^{3}$
A.$\frac{2^{2}}{3}与(\frac{2}{3})^{2}$
B.$-2^{2}与(-2)^{2}$
C.$-(+3)与-|-3|$
D.$(-2)^{3}与-2^{3}$
答案:
B
9. 新考向 数学文化《孙子算经》中记载:“今的形有出门望见九堤,堤有九木,木有九枝,枝有九巢……”大意为:今天出门看见$9$座堤坝,每座堤坝上有$9$棵树,每棵树上有$9$根树枝,每根树枝上有$9$个鸟巢…….文中的鸟巢共有(
A.$9^{3}$个
B.$10^{3}$个
C.$9^{4}$个
D.$10^{4}$个
C
)A.$9^{3}$个
B.$10^{3}$个
C.$9^{4}$个
D.$10^{4}$个
答案:
C
10.(1)当整数$n(n\geqslant1)$为奇数时,$(-1)^{n}=$
(2)当整数$n(n\geqslant1)$为偶数时,$(-1)^{n}=$
(3)对于任意整数$n(n\geqslant1)$,$(-1)^{2n}=$
-1
;(2)当整数$n(n\geqslant1)$为偶数时,$(-1)^{n}=$
1
;(3)对于任意整数$n(n\geqslant1)$,$(-1)^{2n}=$
1
,$(-1)^{2n + 1}=$-1
.
答案:
(1)-1
(2)1
(3)1 -1
(1)-1
(2)1
(3)1 -1
11. 阅读材料:若$a^{b}= N$,则$b = \log_{a}N$,称$b为以a数为底N$的对数,例如$2^{3}= 8$,则$\log_{2}8= \log_{2}2^{3}= 3$.根据材料填空:$\log_{3}9= $
2
.
答案:
2
12. 北师大附属实验校本经典题 如图,将一张边长为$1的正方形纸片分割成7$个部分,部分①的面积是边长为$1$的正方形纸片面积的一半,部分②的面积是部分①面积的一半,部分③的面积是部分②面积的一半,依次类推.
(1)阴影部分的面积是多少?
(2)受(1)的启发,试求出$\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+…+\frac{1}{2^{6}}$的值.
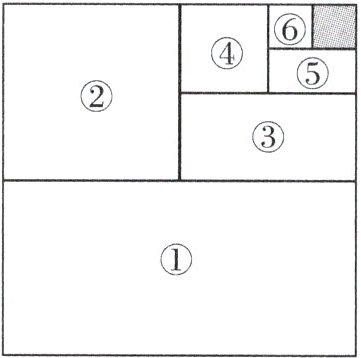
(1)阴影部分的面积是$\frac{1}{2^{6}}=\frac{1}{64}$.
(2)原式$=1-\frac{1}{2^{6}}=1-\frac{1}{64}=\frac{63}{64}$.
(1)阴影部分的面积是多少?
(2)受(1)的启发,试求出$\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+…+\frac{1}{2^{6}}$的值.

(1)阴影部分的面积是$\frac{1}{2^{6}}=\frac{1}{64}$.
(2)原式$=1-\frac{1}{2^{6}}=1-\frac{1}{64}=\frac{63}{64}$.
答案:
解:
(1)阴影部分的面积是$\frac{1}{2^{6}}=\frac{1}{64}$.
(2)原式$=1-\frac{1}{2^{6}}=1-\frac{1}{64}=\frac{63}{64}$.
(1)阴影部分的面积是$\frac{1}{2^{6}}=\frac{1}{64}$.
(2)原式$=1-\frac{1}{2^{6}}=1-\frac{1}{64}=\frac{63}{64}$.
(2024·贵港港南区期中改编)如果 $ |a + 2| + |b - 1| = 0 $,那么 $ (a + b)^{2025} $ 的值为 (
A.-2 025
B.2 025
C.-1
D.1
C
)A.-2 025
B.2 025
C.-1
D.1
答案:
C
已知 $ 2|x - 2| $ 与 $ (y - 3)^2 $ 互为相反数,则 $ |x + y| = $
5
.
答案:
5
若 $ (a + 1)^2 + |b - 3| + |c - 2b| = 0 $,则 $ c - a - b = $
4
.
答案:
4
查看更多完整答案,请扫码查看


