第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
15. 如图,在平面直角坐标系中,直线$y= -x-2$与x轴、y轴分别交于A、B两点,C、D是半径为1的$\odot O$上的两动点,且$CD= \sqrt {2}$,P为弦CD的中点.当C、D两点在圆上运动时,则$\triangle PAB$面积的最大值为______
3
.
答案:
3
16. 如图,在扇形OAB中,$∠AOB= 60^{\circ }$,OD平分$∠AOB交\overset{\frown }{AB}$于点D,C是半径OB上一动点,连接AC、DC.若$OA= 1$,则阴影部分周长的最小值为
$\sqrt{2}+\frac{\pi}{6}$
.
答案:
$\sqrt{2}+\frac{\pi}{6}$
17. [新探究]如图,$Rt\triangle ABC$的内切圆与斜边AB相切于点D,$AD= 4$,$BD= 5$.求$Rt\triangle ABC$的面积.
王小明:这道题算出来面积刚好是20,太凑巧了吧.刚好是$4×5= 20$,有种白算的感觉……
赵丽华:我把4和5换成m、n再算一遍,$\triangle ABC的面积总是m\cdot n$!确实非常神奇……
数学刘老师:大家想一想,既然结果如此简单到极致,不计算能不能得到呢?比如,拼图?
霍佳:刘老师,我在想另一个东西,这个图能不能用尺规画出来啊,感觉图都定了,我怎么想不出来呢?

计算验证
(1)通过计算求出$Rt\triangle ABC$的面积.
拼图演绎
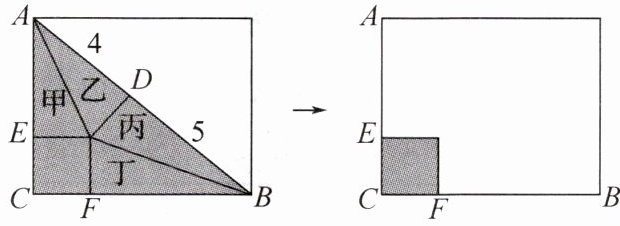
(2)将$Rt\triangle ABC$分割放入矩形中(左图),通过拼图能直接看出“20”.请在下图中画出拼图后的4个直角三角形甲、乙、丙、丁的位置,作必要标注并简要说明.
尺规作图
(3)如图,点D在线段AB上,以AB为斜边求作一个$Rt\triangle ABC$,使它的内切圆与斜边AB相切于点D.(保留作图痕迹,写出必要的文字说明)

王小明:这道题算出来面积刚好是20,太凑巧了吧.刚好是$4×5= 20$,有种白算的感觉……
赵丽华:我把4和5换成m、n再算一遍,$\triangle ABC的面积总是m\cdot n$!确实非常神奇……
数学刘老师:大家想一想,既然结果如此简单到极致,不计算能不能得到呢?比如,拼图?
霍佳:刘老师,我在想另一个东西,这个图能不能用尺规画出来啊,感觉图都定了,我怎么想不出来呢?

计算验证
(1)通过计算求出$Rt\triangle ABC$的面积.
拼图演绎
(2)将$Rt\triangle ABC$分割放入矩形中(左图),通过拼图能直接看出“20”.请在下图中画出拼图后的4个直角三角形甲、乙、丙、丁的位置,作必要标注并简要说明.

尺规作图
(3)如图,点D在线段AB上,以AB为斜边求作一个$Rt\triangle ABC$,使它的内切圆与斜边AB相切于点D.(保留作图痕迹,写出必要的文字说明)

答案:
(1)$S_{\triangle ABC}=20$. (2)略. (3)略.
查看更多完整答案,请扫码查看


