第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
1. (2024苏州阶段测试)阅读材料:若$m^{2}-2mn+2n^{2}-8n+16= 0$,求m、n的值.
解:$\because m^{2}-2mn+2n^{2}-8n+16= 0$,
$\therefore (m^{2}-2mn+n^{2})+(n^{2}-8n+16)= 0,\therefore (m-n)^{2}+(n-4)^{2}= 0$,
$\therefore (m-n)^{2}= 0,(n-4)^{2}= 0,\therefore n= 4,m= 4$.
根据你的观察,探究下面的问题:
(1)已知$x^{2}+2xy+2y^{2}+4y+4= 0$,则$2x+y=$
(2)已知$m-n= 4,mn+k^{2}-6k+13= 0$,则$m+n+k=$
解:$\because m^{2}-2mn+2n^{2}-8n+16= 0$,
$\therefore (m^{2}-2mn+n^{2})+(n^{2}-8n+16)= 0,\therefore (m-n)^{2}+(n-4)^{2}= 0$,
$\therefore (m-n)^{2}= 0,(n-4)^{2}= 0,\therefore n= 4,m= 4$.
根据你的观察,探究下面的问题:
(1)已知$x^{2}+2xy+2y^{2}+4y+4= 0$,则$2x+y=$
2
;(2)已知$m-n= 4,mn+k^{2}-6k+13= 0$,则$m+n+k=$
3
.
答案:
(1)2 (2)3
2. 选取二次三项式$ax^{2}+bx+c(a≠0)$中的两项,配成完全平方式的过程叫配方.
例如:①选取二次项和一次项配方:$x^{2}-4x+9= (x-2)^{2}+5$;
②选取二次项和常数项配方:$x^{2}-4x+9= (x-3)^{2}+2x或x^{2}-4x+9= (x+3)^{2}-10x$;
③选取一次项和常数项配方:$x^{2}-4x+9= (\frac {2}{3}x-3)^{2}+\frac {5}{9}x^{2}$.
根据上述材料,解决下列问题:
(1)求代数式$x^{2}-6x+10$的最小值;
(2)写出代数式$x^{2}-8x+4$的两种不同形式的配方;
(3)已知$x^{2}+y^{2}+xy-3y+3= 0$,求$x^{y}$的值.
例如:①选取二次项和一次项配方:$x^{2}-4x+9= (x-2)^{2}+5$;
②选取二次项和常数项配方:$x^{2}-4x+9= (x-3)^{2}+2x或x^{2}-4x+9= (x+3)^{2}-10x$;
③选取一次项和常数项配方:$x^{2}-4x+9= (\frac {2}{3}x-3)^{2}+\frac {5}{9}x^{2}$.
根据上述材料,解决下列问题:
(1)求代数式$x^{2}-6x+10$的最小值;
(2)写出代数式$x^{2}-8x+4$的两种不同形式的配方;
(3)已知$x^{2}+y^{2}+xy-3y+3= 0$,求$x^{y}$的值.
答案:
(1)1. (2)$(x-4)^{2}-12$或$(x-2)^{2}-4x$(答案不唯一).(3)$x^{y}=1$.
3. 我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用.例如:已知x可取任何实数,试求二次三项式$x^{2}+2x+3$的最小值.
解:$x^{2}+2x+3= x^{2}+2x+1+2= (x+1)^{2}+2$.
$\because$无论x取何实数,都有$(x+1)^{2}≥0$,
$\therefore (x+1)^{2}+2≥2$,即$x^{2}+2x+3$的最小值为2.
(1)请直接写出$2x^{2}+4x+10$的最小值:
(2)求证:无论x取何实数,二次根式$\sqrt {x^{2}+x+2}$都有意义;
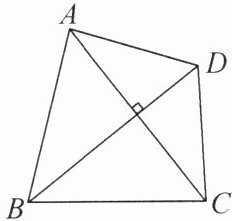
(3)如图,在四边形ABCD中,$AC⊥BD$,若$AC+BD= 10$,求四边形ABCD面积的最大值.
解:$x^{2}+2x+3= x^{2}+2x+1+2= (x+1)^{2}+2$.
$\because$无论x取何实数,都有$(x+1)^{2}≥0$,
$\therefore (x+1)^{2}+2≥2$,即$x^{2}+2x+3$的最小值为2.
(1)请直接写出$2x^{2}+4x+10$的最小值:
8
;(2)求证:无论x取何实数,二次根式$\sqrt {x^{2}+x+2}$都有意义;
证明略.
(3)如图,在四边形ABCD中,$AC⊥BD$,若$AC+BD= 10$,求四边形ABCD面积的最大值.

四边形ABCD面积的最大值为$\frac{25}{2}$.
答案:
(1)8 (2)证明略.(3)四边形ABCD面积的最大值为$\frac{25}{2}$.
查看更多完整答案,请扫码查看


