《2025年夺冠课课练九年级数学上册苏科版》

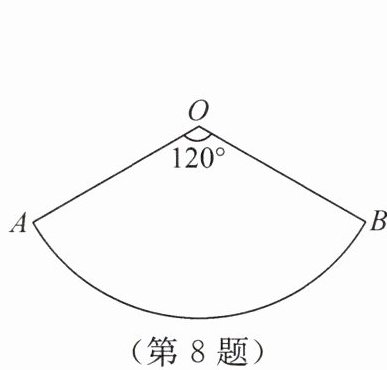
8. 如图,扇形$OAB$是一个圆锥的侧面展开图,$\angle AOB = 120^{\circ}$,$\overgroup{AB}的长为6\pi cm$,则该圆锥的侧面积为(C)

A.$6\pi cm^{2}$
B.$18\pi cm^{2}$
C.$27\pi cm^{2}$
D.$54\pi cm^{2}$

答案： C

9. 若圆锥的母线长为13cm,侧面展开图的面积为$65\pi cm^{2}$,则这个圆锥的高为12 cm。

答案： 12 cm

10. 如图,在一张正方形纸片上剪下一个半径为$r的圆形和一个半径为R$的扇形,使之恰好围成图中所示的圆锥,则$R与r$之间的关系是$R=4r$。

答案： $R=4r$

11. (2024淮安模拟)如图,小珍同学用半径为10cm,圆心角为$100^{\circ}$的扇形纸片,制作一个底面半径为2.5cm的圆锥侧面,则圆锥上粘贴部分的面积是____$cm^{2}$。

答案： $\frac{25}{9}\pi$

12. 在数学实验课上,小莹将含$30^{\circ}$角的直角三角尺分别以两个直角边为轴旋转一周,得到甲、乙两个圆锥,并用作图软件Geogebra画出如图所示的示意图.
小亮观察后说:“甲、乙圆锥的侧面都是由三角尺的斜边$AB$旋转得到,所以它们的侧面积相等.”
你认同小亮的说法吗? 请说明理由.

答案： 不认同

13. 如图,物体由两个圆锥组成,其主视图中,$\angle A = 90^{\circ}$,$\angle ABC = 105^{\circ}$. 若上面圆锥的侧面积为1,则下面圆锥的侧面积为(D)
A.2
B.$\sqrt{3}$
C.$\frac{3}{2}$
D.$\sqrt{2}$

答案： D

14. 如图,在半径为$\sqrt{2}$的圆形纸片中,剪一个圆心角为$90^{\circ}$的最大扇形(阴影部分),则这个扇形的面积为$\pi$；若将此扇形围成一个无底的圆锥(不计接头),则圆锥的底面半径为$\frac{1}{2}$。

答案： $\pi$ $\frac{1}{2}$