第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
3.(2024·河南)为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下图表.
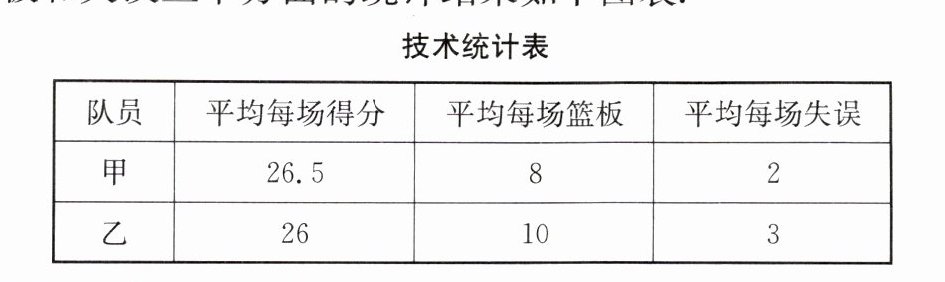

根据以上信息,解答下列问题.
(1)这六场比赛中,得分更稳定的队员是______(填"甲"或"乙");甲队员得分的中位数为27.5分,乙队员得分的中位数为______分;
(2)请从得分方面分析,这六场比赛中,甲、乙两名队员谁的表现更好;
(3)规定"综合得分"为平均每场得分×1+平均每场篮板×1.5+平均每场失误×(-1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
(1)
(2)
(3)


根据以上信息,解答下列问题.
(1)这六场比赛中,得分更稳定的队员是______(填"甲"或"乙");甲队员得分的中位数为27.5分,乙队员得分的中位数为______分;
(2)请从得分方面分析,这六场比赛中,甲、乙两名队员谁的表现更好;
(3)规定"综合得分"为平均每场得分×1+平均每场篮板×1.5+平均每场失误×(-1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
(1)
甲
29
(2)
解:因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好.(答案不唯一)
(3)
解:甲的综合得分为$26.5×1+8×1.5+2×(-1)=36.5$(分),乙的综合得分为$26×1+10×1.5+3×(-1)=38$(分),因为$38>36.5$,所以乙队员表现更好.
答案:
3.
(1)甲 29
(2)解:因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好.(答案不唯一)
(3)解:甲的综合得分为$26.5×1+8×1.5+2×(-1)=36.5$(分),乙的综合得分为$26×1+10×1.5+3×(-1)=38$(分),因为$38>36.5$,所以乙队员表现更好.
(1)甲 29
(2)解:因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好.(答案不唯一)
(3)解:甲的综合得分为$26.5×1+8×1.5+2×(-1)=36.5$(分),乙的综合得分为$26×1+10×1.5+3×(-1)=38$(分),因为$38>36.5$,所以乙队员表现更好.
4.某校深入开展了以"珍爱生命 谨防溺水"为主题的安全教育活动,并在九年级举办了防溺水知识竞赛,从两班各随机抽取了10名学生的成绩(单位:分),整理如下:(成绩用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100)
九年级(1)班10名学生的成绩是:96,80,96,86,99,98,92,100,91,82.
九年级(2)班10名学生的成绩在C组中的数据是:94,90,92.
通过数据分析,结果如下图表:
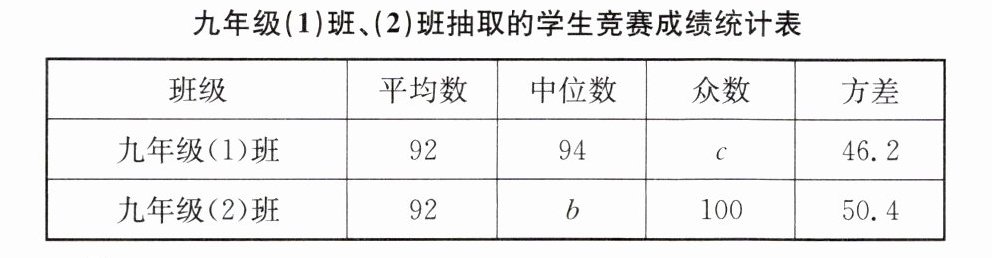

根据以上信息,解答下列问题:
(1)a= ______
(2)学校欲选派成绩更稳定的班级参加下一阶段的活动,根据表格中的数据,学校会选派哪一个班级?请说明理由;
(3)九年级两个班共有80人参加了此次活动,估计两个班参加此次活动成绩优秀(x≥90)的学生总人数.
九年级(1)班10名学生的成绩是:96,80,96,86,99,98,92,100,91,82.
九年级(2)班10名学生的成绩在C组中的数据是:94,90,92.
通过数据分析,结果如下图表:


根据以上信息,解答下列问题:
(1)a= ______
40
,b= ______93
,c= ______96
;(2)学校欲选派成绩更稳定的班级参加下一阶段的活动,根据表格中的数据,学校会选派哪一个班级?请说明理由;
解:选派九年级(1)班,理由如下:∵两个班的平均成绩相同,而九年级(1)班的方差为46.2,九年级(2)班的方差为50.4,∴九年级(1)班成绩更稳定,∴学校会选派九年级(1)班.
(3)九年级两个班共有80人参加了此次活动,估计两个班参加此次活动成绩优秀(x≥90)的学生总人数.
解:九年级(2)班D组的人数为$10×40\% =4$(人),成绩优秀的有7人,九年级(1)班10名学生中成绩优秀的有7人.∴估计参加此次调查活动成绩优秀($x\geq90$)的九年级学生人数是$80×\frac{7+7}{20}=56$(人).
答案:
4.
(1)40 93 96
(2)解:选派九年级
(1)班,理由如下:
∵两个班的平均成绩相同,而九年级
(1)班的方差为46.2,九年级
(2)班的方差为50.4,
∴九年级
(1)班成绩更稳定,
∴学校会选派九年级
(1)班.
(3)解:九年级
(2)班D组的人数为$10×40\% =4$(人),成绩优秀的有7人,九年级
(1)班10名学生中成绩优秀的有7人.
∴估计参加此次调查活动成绩优秀($x\geq90$)的九年级学生人数是$80×\frac{7+7}{20}=56$(人).
(1)40 93 96
(2)解:选派九年级
(1)班,理由如下:
∵两个班的平均成绩相同,而九年级
(1)班的方差为46.2,九年级
(2)班的方差为50.4,
∴九年级
(1)班成绩更稳定,
∴学校会选派九年级
(1)班.
(3)解:九年级
(2)班D组的人数为$10×40\% =4$(人),成绩优秀的有7人,九年级
(1)班10名学生中成绩优秀的有7人.
∴估计参加此次调查活动成绩优秀($x\geq90$)的九年级学生人数是$80×\frac{7+7}{20}=56$(人).
查看更多完整答案,请扫码查看


