第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1. 脆蜜金桔是地方名果,是柳州市融安县的特产之一.请你运用数学知识,根据素材,帮果农解决问题.
|信息及素材|
|素材一|在专业种植技术人员的正确指导下,果农对脆蜜金桔种植技术进行了研究与改进,使产量得到了增长,根据果农们的记录,2020年脆蜜金桔平均每株产量是13千克,2022年达到了15.6千克,每年的增长率基本相同|
|素材二|脆蜜金桔一般用长方体包装盒包装后进行售卖|
|素材三|果农们通过调查发现,顾客们也很愿意购买美观漂亮的其他造型的包装纸盒|
任务1:设脆蜜金桔产量的年平均增长率为$x$,依题意列方程得______;
任务2:现有长80cm,宽75cm的长方形纸板,将四角各裁掉一个正方形(如图①),折成无盖长方体纸盒(如图②).为了放下适当数量的脆蜜金桔,需要设计底面积为$3300cm^{2}$的纸盒,计算此时纸盒的高;
任务3:为了增加包装盒的种类,打算将任务2中的纸板通过图③的方式裁剪,得到底面为正六边形的无盖纸盒(如图④),求出此时纸盒的高.(图中实线表示剪切线,虚线表示折痕.纸板厚度及剪切接缝处损耗忽略不计)

|信息及素材|
|素材一|在专业种植技术人员的正确指导下,果农对脆蜜金桔种植技术进行了研究与改进,使产量得到了增长,根据果农们的记录,2020年脆蜜金桔平均每株产量是13千克,2022年达到了15.6千克,每年的增长率基本相同|
|素材二|脆蜜金桔一般用长方体包装盒包装后进行售卖|
|素材三|果农们通过调查发现,顾客们也很愿意购买美观漂亮的其他造型的包装纸盒|
任务1:设脆蜜金桔产量的年平均增长率为$x$,依题意列方程得______;
任务2:现有长80cm,宽75cm的长方形纸板,将四角各裁掉一个正方形(如图①),折成无盖长方体纸盒(如图②).为了放下适当数量的脆蜜金桔,需要设计底面积为$3300cm^{2}$的纸盒,计算此时纸盒的高;
任务3:为了增加包装盒的种类,打算将任务2中的纸板通过图③的方式裁剪,得到底面为正六边形的无盖纸盒(如图④),求出此时纸盒的高.(图中实线表示剪切线,虚线表示折痕.纸板厚度及剪切接缝处损耗忽略不计)

答案:
任务1:13(1+x)²=15.6
任务2:解:设裁掉正方形的边长为m cm,
由题意得(75−2m)×(80−2m)=3300,
解得m₁=10,m₂=135/2(不符合题意,舍去).
答:此时纸盒的高为10 cm.
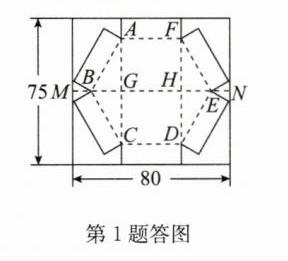
任务3:解:如答图,设底面正六边形为ABCDEF,连接AC,FD,BE,AC和BE交于点G,FD和BE交于点H,BE所在直线交长方形纸板的边于点M,N.设底面正六边形的边长为a cm,纸盒的高为b cm.
∵正六边形的每条边相等,每个内角都为120°,
∴△ABC为等腰三角形,∠ABC=120°,
∴∠BAC=∠BCA=30°,由正六边形的性质可得BE平分∠ABC,
∴∠ABE=60°,
∴∠AGB=90°,
∴直角三角形ABG中,BG=1/2a,AG=√3/2a,同理可得直角三角形FHE中,HE=1/2a,
∵CG=AG=√3/2a,b+AG+GC+b=75,
∴2b+√3a=75①.
∵左侧小三角形顶点B的角度=360°−120°−90°−90°=60°,
∴左侧小三角形是边长为b的等边三角形.
根据图形上下对称可得MN与长方形纸板的左右两边垂直,
∴BM为等边三角形的高,
∴BM=√3/2b,
同理可得,EN=BM=√3/2b.
易知四边形AGHF为矩形,
∴GH=AF=a.
∵MN=MB+BG+GH+HE+EN=80,
∴2a+√3b=80②.
联立①②式可得b=150−80√3
答:纸盒的高为(150−80√3)cm.
任务1:13(1+x)²=15.6
任务2:解:设裁掉正方形的边长为m cm,
由题意得(75−2m)×(80−2m)=3300,
解得m₁=10,m₂=135/2(不符合题意,舍去).
答:此时纸盒的高为10 cm.
任务3:解:如答图,设底面正六边形为ABCDEF,连接AC,FD,BE,AC和BE交于点G,FD和BE交于点H,BE所在直线交长方形纸板的边于点M,N.设底面正六边形的边长为a cm,纸盒的高为b cm.
∵正六边形的每条边相等,每个内角都为120°,
∴△ABC为等腰三角形,∠ABC=120°,
∴∠BAC=∠BCA=30°,由正六边形的性质可得BE平分∠ABC,
∴∠ABE=60°,
∴∠AGB=90°,
∴直角三角形ABG中,BG=1/2a,AG=√3/2a,同理可得直角三角形FHE中,HE=1/2a,
∵CG=AG=√3/2a,b+AG+GC+b=75,
∴2b+√3a=75①.
∵左侧小三角形顶点B的角度=360°−120°−90°−90°=60°,
∴左侧小三角形是边长为b的等边三角形.
根据图形上下对称可得MN与长方形纸板的左右两边垂直,
∴BM为等边三角形的高,
∴BM=√3/2b,
同理可得,EN=BM=√3/2b.
易知四边形AGHF为矩形,
∴GH=AF=a.
∵MN=MB+BG+GH+HE+EN=80,
∴2a+√3b=80②.
联立①②式可得b=150−80√3
答:纸盒的高为(150−80√3)cm.

查看更多完整答案,请扫码查看


