第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
6. 下列图形中,四个顶点一定在同一个圆上的是 (
A.菱形
B.平行四边形
C.矩形
D.一般的四边形
C
)A.菱形
B.平行四边形
C.矩形
D.一般的四边形
答案:
C
7. 如图,$\odot A$的半径为3,圆心A的坐标为$(1,0)$,点$B(m,0)$在$\odot A$外,则m的取值范围是 (
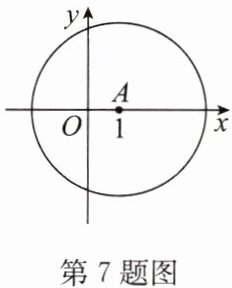
A.$m<4$
B.$m>-2$
C.$-2<m<4$
D.$m<-2或m>4$
D
)
A.$m<4$
B.$m>-2$
C.$-2<m<4$
D.$m<-2或m>4$
答案:
D
8. 已知点P不在$\odot O$上,若点P到$\odot O$上的点的最小距离是4 cm,最大距离是9 cm,则$\odot O$的半径是
6.5cm或2.5cm
.
答案:
6.5cm或2.5cm
9. 在平面直角坐标系中,以点$M(0,3)$为圆心,5为半径画圆,点B的坐标为$(a,0)$.
(1)若点B在圆上,则$a= $
(2)若点B在圆外,则a的取值范围是
(1)若点B在圆上,则$a= $
±4
;(2)若点B在圆外,则a的取值范围是
a>4或a<−4
.
答案:
(1)±4
(2)a>4或a<−4
(1)±4
(2)a>4或a<−4
10. 如图,在$\triangle ABC$中,$∠C= 90^{\circ },BC= 6,AC= 8$,N是AB边的中点,D,E分别是边AC,BC上的动点,始终保持$DE= 5$,M是DE的中点,则MN的最小值为______
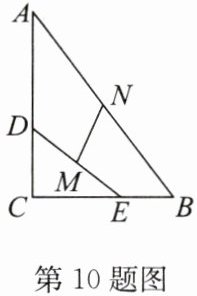
2.5
.
答案:
2.5
11. (2024·宿城期中)如图,在$\triangle ABC$中,$AB= AC= 2\sqrt {5},BC= 4$,点D是AB的中点,若以点D为圆心,r为半径作$\odot D$,使点B在$\odot D$内,点C在$\odot D$外,试求r的取值范围.
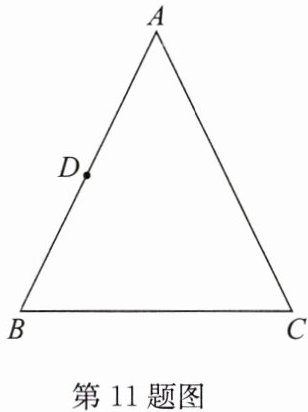

答案:
解:如答图,连接CD,过点A作AE⊥BC于点E,过点D作DF⊥BC于点F,显然DF//AE.
∵AB=AC=2√5,BC=4,
∴BE=1/2BC=2,
∴AE=√(AB²-BE²)=4.
∵点D是AB的中点,
∴DF是△ABE的中位线,
∴DF=1/2AE=2,BF=1/2BE=1,
∴CF=3,
∴CD=√(DF²+CF²)=√13,又DB=1/2AB=√5,
∴r的取值范围是√5<r<√13

解:如答图,连接CD,过点A作AE⊥BC于点E,过点D作DF⊥BC于点F,显然DF//AE.
∵AB=AC=2√5,BC=4,
∴BE=1/2BC=2,
∴AE=√(AB²-BE²)=4.
∵点D是AB的中点,
∴DF是△ABE的中位线,
∴DF=1/2AE=2,BF=1/2BE=1,
∴CF=3,
∴CD=√(DF²+CF²)=√13,又DB=1/2AB=√5,
∴r的取值范围是√5<r<√13

12. 如图,在矩形ABCD中,已知$AB= 3,BC= 4$,点P是BC边上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,求线段MC的最小值.


答案:
解:如答图,连接AM.

∵点B和点M关于AP对称,
∴AB=AM=3,
∴点M在以点A为圆心,3为半径的圆上,
∴当A,M,C三点共线时,CM最短,
∵AC=√(3²+4²)=5,AM=AB=3,
∴CM=5−3=2.
∴线段MC的最小值为2.
解:如答图,连接AM.

∵点B和点M关于AP对称,
∴AB=AM=3,
∴点M在以点A为圆心,3为半径的圆上,
∴当A,M,C三点共线时,CM最短,
∵AC=√(3²+4²)=5,AM=AB=3,
∴CM=5−3=2.
∴线段MC的最小值为2.
查看更多完整答案,请扫码查看


