《2025年启东中学作业本九年级数学上册苏科版宿迁专版》

8. (2023·无锡期中)如图,点O是正六边形ABCDEF对角线DF上的一点,且$S_{\triangle AOC}= 8$,则正六边形ABCDEF的面积为 (B)

A.18
B.24
C.30
D.随着点O的变化而变化

答案： B

9. 如图,正四边形ABCD和正五边形CEFGH内接于$\odot O$,AD和EF相交于点M,则$∠AMF$的度数为 (B)
A.$26^{\circ}$
B.$27^{\circ}$
C.$28^{\circ}$
D.$30^{\circ}$

答案： B

10. 如图,在正八边形ABCDEFGH中,连接AC,AE.
(1)$∠CAE=$45$^{\circ}$;
(2)若$AE= 4$,则$AC=$$2\sqrt{2}$.

答案：
(1)45　
(2)$2\sqrt{2}$

11. 如图,在正六边形ABCDEF中,$AB= 6$,点M在边AF上,且$AM= 2$. 若经过点M的直线l将正六边形的面积平分,则直线l被正六边形所截得的线段长是____$4\sqrt{7}$.

答案： $4\sqrt{7}$

12. 如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且$BM= CN$,AM交BN于点P.
(1)求证:$\triangle ABM\cong \triangle BCN$;
(2)求$∠APN$的度数.

答案：
(1)证明:
∵五边形ABCDE是正五边形，
∴AB=BC,∠ABM=∠BCN.在△ABM和△BCN中,$\begin{cases} AB=BC, \\ ∠ABM=∠BCN, \\ BM=CN, \end{cases}$
∴△ABM≌△BCN(SAS).　
(2)解:
∵△ABM≌△BCN,
∴∠MBP=∠BAP.
∵∠MBP+∠BMP+∠BPM=180°∠BAP+∠BMA+∠MBA=180°,
∴∠BPM=∠MBA.
∵∠BPM=∠APN,
∴∠APN=∠MBA=$\frac{(5-2)×180°}{5}=108°$.

13. 如图,在边长为2 cm的正六边形ABCDEF中,点P在BC边上,求$\triangle PEF$的面积.

答案：
解:如答图，连接BE,BF.
∵多边形ABCDEF是正六边形，
∴∠ABC=∠BAF=∠AFE=120°,且AB=AF.
∴∠ABF=∠AFB=30°,
∴∠CBF=∠EFB=90°.
∴BC//EF,
∴$S_{\triangle PEF}=S_{\triangle BEF}$.
∵直线BE是正六边形ABCDEF的对称轴，
∴∠ABE=$\frac{1}{2}$∠ABC=60°.
∴∠EBF=∠ABE-∠ABF=30°.
∴BF=$\sqrt{3}$EF=$2\sqrt{3}$(cm).
∴$S_{\triangle PEF}=S_{\triangle BEF}=\frac{1}{2}EF·BF=\frac{1}{2}×2×2\sqrt{3}=2\sqrt{3}$(cm²).　　　　　　　　

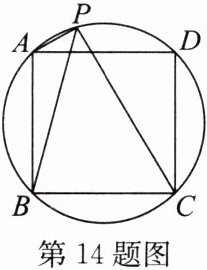
14. 如图,已知P为正方形ABCD的外接圆的$\overset{\frown}{AD}$上任意一点,求证:$\frac{PA+PC}{PB}$为定值.

答案：
证明:如答图，延长PA到点E,使AE=PC,连接BE.
∵∠BAE+∠BAP=180°,∠BAP+∠PCB=180°,
∴∠BAE=∠PCB,
∵四边形ABCD是正方形，
∴AB=BC,∠ABC=90°,在△ABE和△CBP中,$\begin{cases} AB=BC, \\ ∠BAE=∠PCB, \\ AE=CP, \end{cases}$
∴△ABE≌△CBP(SAS),
∴∠ABE=∠CBP,BE=BP,
∴∠ABE+∠ABP=∠ABP+∠CBP=90°,
∴△BEP是等腰直角三角形，
∴PA+PC=PE=$\sqrt{2}$PB.即$\frac{PA+PC}{PB}=\sqrt{2}$,
∴$\frac{PA+PC}{PB}$为定值.