第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
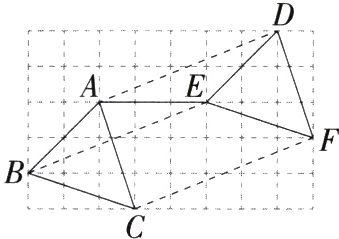
9.(2024福建莆田期中,6,★☆☆)如图,将△ABC沿着某一方向平移一定的距离得到△DEF,连接AE,则下列的结论:①AD=CF;②AC//DF;③∠ABC=∠DEF;④∠DAE=∠AEB.其中正确的为(M7207008) ( )
A.①②③④
B.①②③
C.①②④
D.①②

A.①②③④
B.①②③
C.①②④
D.①②
答案:
A 由平移的性质可得AD = CF,AC//DF,∠ABC = ∠DEF,AD//BE,
∴ ∠DAE = ∠AEB,
∴ 结论①②③④均正确,故选A。
∴ ∠DAE = ∠AEB,
∴ 结论①②③④均正确,故选A。
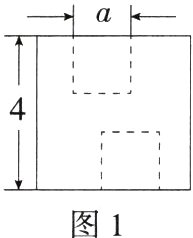
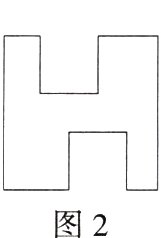
10.(2024山东威海芝罘期末,10,★☆☆)如图1,从一个边长为4的正方形中剪掉两个边长为a的正方形得到如图2所示的图形,若图2中图形的周长为22,则a的值是(M7207008) ( )
A.1
B.1.5
C.2
D.3


A.1
B.1.5
C.2
D.3
答案:
B 由题意易知,题图2中图形的周长比题图1中图形的周长多4a。
∵ 题图2中图形的周长为22,
∴ 4×4 + 4a = 22,解得a = 1.5。故选B。
∵ 题图2中图形的周长为22,
∴ 4×4 + 4a = 22,解得a = 1.5。故选B。
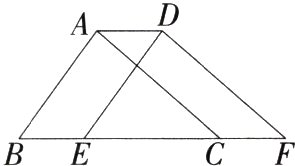
11.(2024天津宁河月考,10,★☆☆)如图,将周长为8的△ABC沿BC方向平移2个单位长度得到△DEF,则四边形ABFD的周长为(M7207008) ( )

A.12
B.15
C.17
D.21


A.12
B.15
C.17
D.21
答案:
A
∵ $\triangle ABC$沿BC方向平移2个单位长度得到$\triangle DEF$,
∴ DF = AC,AD = CF = 2,
∴ 四边形ABFD的周长=AB + BF + DF + AD = AB + BC + CF + AC + AD=$\triangle ABC$的周长+AD + CF = 8 + 2 + 2 = 12。故选A。
∵ $\triangle ABC$沿BC方向平移2个单位长度得到$\triangle DEF$,
∴ DF = AC,AD = CF = 2,
∴ 四边形ABFD的周长=AB + BF + DF + AD = AB + BC + CF + AC + AD=$\triangle ABC$的周长+AD + CF = 8 + 2 + 2 = 12。故选A。
12.易错题(2023河北石家庄裕华期中,16,★☆☆)如图,在三角形ABC中,BC=8cm.将三角形ABC沿BC所在直线向右平移一定的距离得到三角形DEF,若要使AD=3CE成立,则平移的距离是 ( )

A.6cm
B.9cm
C.6cm或12cm
D.9cm或12cm

A.6cm
B.9cm
C.6cm或12cm
D.9cm或12cm
答案:
C ①当点E在点C右侧时,
∵ AD = BE = BC + CE = 3CE,
∴ BC = 2CE,
∵ BC = 8 cm,
∴ CE = 4 cm,
∴ AD = 12 cm,
∴ 平移的距离是12 cm;
②当点E在点B,C之间时,
∵ AD = BE = 3CE,
∴ BC = BE + CE = BE+$\frac{1}{3}$BE=$\frac{4}{3}$BE,
∵ BC = 8 cm,
∴ BE = 6 cm,
∴ AD = 6 cm,
∴ 平移的距离是6 cm。
综上,平移的距离是12 cm或6 cm。故选C。
易错警示
本题容易被所给图形误导,漏掉点E在点C右侧的情况。
∵ AD = BE = BC + CE = 3CE,
∴ BC = 2CE,
∵ BC = 8 cm,
∴ CE = 4 cm,
∴ AD = 12 cm,
∴ 平移的距离是12 cm;
②当点E在点B,C之间时,
∵ AD = BE = 3CE,
∴ BC = BE + CE = BE+$\frac{1}{3}$BE=$\frac{4}{3}$BE,
∵ BC = 8 cm,
∴ BE = 6 cm,
∴ AD = 6 cm,
∴ 平移的距离是6 cm。
综上,平移的距离是12 cm或6 cm。故选C。
易错警示
本题容易被所给图形误导,漏掉点E在点C右侧的情况。
13.[新考向·项目式学习试题]推理能力 图形操作:图1、图2中的长方形的长均为10米,宽均为5米,在图1中,将线段AB向上平移1米到A'B',得到封闭图形AA'B'B(阴影部分).在图2中,将折线ABC(其中点B叫作折线ABC的一个"折点")向上平移1米到折线A'B'C',得到封闭图形AA'B'C'CB(阴影部分).(M7207008)
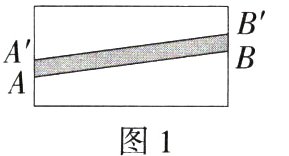
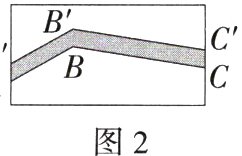
(1)问题解决:设图1,图2中除去阴影部分后剩下部分的面积分别为S₁,S₂,则S₁=________平方米;并比较大小:S₁________S₂(填">""="或"<").
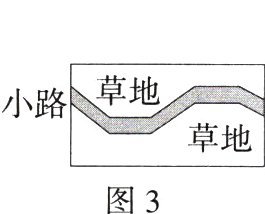
(2)联想探索:如图3,在一块长方形草地上,有一条弯折的柏油小路(小路的宽度是1米),长方形的长为a米,宽为b米,请你直接写出草地(空白部分)的面积是________平方米(用含a,b的式子表示).
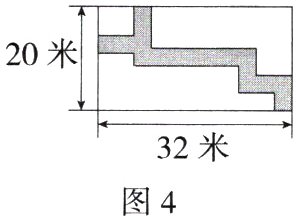
(3)实际运用:如图4,在长方形地块内修筑同样宽的两条相交的道路(道路与长方形的边平行或垂直),余下部分作为耕地,若道路宽为4米,则剩余的耕地面积为________平方米.


(1)问题解决:设图1,图2中除去阴影部分后剩下部分的面积分别为S₁,S₂,则S₁=________平方米;并比较大小:S₁________S₂(填">""="或"<").
(2)联想探索:如图3,在一块长方形草地上,有一条弯折的柏油小路(小路的宽度是1米),长方形的长为a米,宽为b米,请你直接写出草地(空白部分)的面积是________平方米(用含a,b的式子表示).

(3)实际运用:如图4,在长方形地块内修筑同样宽的两条相交的道路(道路与长方形的边平行或垂直),余下部分作为耕地,若道路宽为4米,则剩余的耕地面积为________平方米.

答案:
答案
(1)40;=
(2)a(b - 1)(或(ab - a))
(3)448
解析
(1)根据题意得$S_{1}=10×(5 - 1)=10×4 = 40$(平方米),$S_{2}=10×(5 - 1)=10×4 = 40$(平方米),
∴ $S_{1}=S_{2}$。
(2)在题图3中,长方形的长为a米,宽为b米,小路的宽度是1米,
∴ 草地(空白部分)的面积是a(b - 1)=(ab - a)平方米。
(3)在题图4中,长方形的长为32米,宽为20米,道路宽为4米,
∴ 剩余的耕地面积是(32 - 4)×(20 - 4)= 448(平方米)。
(1)40;=
(2)a(b - 1)(或(ab - a))
(3)448
解析
(1)根据题意得$S_{1}=10×(5 - 1)=10×4 = 40$(平方米),$S_{2}=10×(5 - 1)=10×4 = 40$(平方米),
∴ $S_{1}=S_{2}$。
(2)在题图3中,长方形的长为a米,宽为b米,小路的宽度是1米,
∴ 草地(空白部分)的面积是a(b - 1)=(ab - a)平方米。
(3)在题图4中,长方形的长为32米,宽为20米,道路宽为4米,
∴ 剩余的耕地面积是(32 - 4)×(20 - 4)= 448(平方米)。
查看更多完整答案,请扫码查看


