《2025年5年中考3年模拟七年级数学下册人教版》

18.[答案含评分细则](2023天津南开期末)(8分)已知7和3−2x是一个正整数α的互不相等的两个平方根.(M7208001)
(1)求a的值以及x的值.
(2)求22−3a的立方根.

答案： 解析
(1)$\because7$和$3 - 2x$是一个正整数$a$的互不相等的两个平方根，
$\therefore3 - 2x=-7$，$a = 7^{2}=49$，$\therefore x = 5$.
综上，$a$的值为49，$x$的值为5. ………………… 4分
(2)$22-3a = 22-3\times49 = 22-147=-125$，
$\therefore22 - 3a$的立方根是$-5$. …………………… 8分

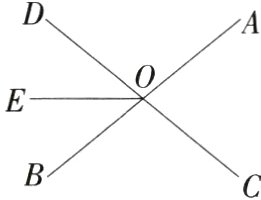
19.[答案含评分细则(2024河南师大附中期中)(8 分)如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.(M7207001)
(1)图中∠AOD的对顶角为________,∠BOE 的邻补角为________.
(2)若OE平分∠BOD,∠DOE:∠AOD=1:4,求∠EOC和∠BOC的度数.

答案： 解析
(1)$\angle BOC$；$\angle AOE$. ………………… 2分
(2)设$\angle DOE=x^{\circ}$，则$\angle AOD = 4x^{\circ}$， …………… 3分
$\because OE$平分$\angle BOD$，$\therefore\angle BOE=\angle DOE=x^{\circ}$， …… 4分
$\therefore x^{\circ}+x^{\circ}+4x^{\circ}=180^{\circ}$，解得$x = 30$， …………… 5分
$\therefore\angle DOE=\angle BOE = 30^{\circ}$，$\angle AOD = 4x^{\circ}=120^{\circ}$， ……
$\therefore\angle BOC=\angle AOD = 120^{\circ}$，$\angle EOC = 180^{\circ}-\angle DOE = 150^{\circ}$. ……………………………………… 8分

20.[答案含评分细则](2024湖南宁乡期末)(8分)如图所示的是某校的平面示意图,如以正东为x 轴正方向,正北为y轴正方向建立平面直角坐标系后,得到初中楼的坐标是(−4,2),实验楼的坐标是(−4,0).(M7209003)
(1)坐标原点为________的位置.
(2)在图中画出此平面直角坐标系.
(3)校门在第________象限,图书馆的坐标是________,操场的坐标是________.
(4)若宿舍楼的坐标是(−3,−2),请在图上标出来.

答案：
解析
(1)坐标原点为高中楼的位置. ……… 2分
(2)根据坐标原点在高中楼处，建立平面直角坐标系，如图所示. ………………………………… 4分

(3)由平面直角坐标系可知，校门在第四象限，图书馆的坐标为$(4,1)$，操场的坐标为$(1,3)$. …… 7分
(4)宿舍楼的位置如图所示. ………………… 8分