《2025年5年中考3年模拟七年级数学下册人教版》

9.(2023北京海淀期中改编)如图,面积为7的正方形ABCD的顶点A在数轴上,且点A表示的数为1,若点E在数轴上(点E在点A的左侧)且AB=AE,则点E所表示的数为(M7208002)(　　　)

A.1−$\sqrt{7}$　
　B.2−$\sqrt{7}$　
　C.−$\sqrt{7}$　
　D.$\sqrt{7}$

答案： A $\because$正方形$ABCD$的面积为7，$\therefore AB^{2}=7$，
$\therefore AB=\sqrt{7}$，$\therefore AE = AB=\sqrt{7}$.$\because$点$A$表示的数为1，
$\therefore$点$E$表示的数为$1-\sqrt{7}$.故选A.

10.新考向.规律探究试题(2024江西南昌期末)如图,在平面直角坐标系xOy中,动点P按图中箭头所示的方向依次运动,第1次从点(−1,0)运动到点(0,1),第2次运动到点(1,0),第3次运动到点(2,−2)，……,按这样的运动规律,动点P第2024次运动到点(M7209004)　(　　　)

A.(2023,0)　　　　
　B.(2024,−2)
C.(2023,1)　　　　
　D.(2024,0)

答案： A 点$P$的运动规律是每运动4次向右平移4个单位，$\because2024\div4 = 506$，$\therefore$动点$P$第2024次运动后，共向右平移$506\times4 = 2024$个单位，$\therefore$点$P$第2024次运动到点$(2023,0)$，故选A.

11.(2024广东惠州二模)在平面直角坐标系中,点M(2m,m+1)在y轴上,则m=__________.(M7209002)

答案： 答案 0
解析 $\because$点$M(2m,m + 1)$在$y$轴上，$\therefore2m = 0$，
解得$m = 0$.

12.比较大小:$\frac{\sqrt{7}}{2}$________$\sqrt{3}$.(M7208003)

答案： 答案 ＜
解析 $(\frac{\sqrt{7}}{2})^2=\frac{7}{4}$，$(\sqrt{3})^2 = 3$，$\because\frac{7}{4}＜3$，$\therefore\frac{\sqrt{7}}{2}＜\sqrt{3}$.

13.新独家原创]能说明“带根号的数是无理数”是假命题的一个反例是________.

答案： 答案 $\sqrt{4}$(答案不唯一)

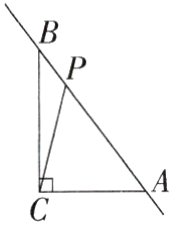
14.(2023山东聊城东阿期末)如图,△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,P为直线AB上一动点,连接PC,则线段PC长度的最小值是________.(M7207002)

答案： 答案 $\frac{24}{5}$
解析 在$\triangle ABC$中，$\angle ACB = 90^{\circ}$，$AC = 6$，$BC = 8$，$AB = 10$，当$PC\perp AB$时，线段$PC$的长度最小，
此时$\frac{1}{2}AB\cdot PC=\frac{1}{2}AC\cdot BC$，$\therefore PC=\frac{24}{5}$.

15.(2023新疆乌鲁木齐天山二模)如图,直角三角形的直角顶点在直尺的一边上,若∠1=29°,∠2 =126°,则∠3等于________°.(M7207006)

答案：
答案 25
解析 如图，根据题意可知$CD// EF$，过点$A$作$AB// CD$，则$\angle3=\angle4$，$AB// EF$.
$\therefore\angle BAC+\angle2 = 180^{\circ}$，即$\angle4+\angle1+\angle2 = 180^{\circ}$.
$\because\angle1 = 29^{\circ}$，$\angle2 = 126^{\circ}$，
$\therefore\angle4+29^{\circ}+126^{\circ}=180^{\circ}$.
$\therefore\angle4 = 25^{\circ}$.$\therefore\angle3 = 25^{\circ}$.

16.(2024湖南长沙天心月考)如图,E在线段BA的延长线上,∠EAD=∠D,∠B=∠D,EF//HC,连接FH交AD于G,∠FGA的余角比∠DGH 大16°,K为线段BC上一点,连接CG,使∠CKG=∠CGK,在∠AGK内部有射线GM,GM 平分∠FGC.则下列结论:①AD//BC;②GK平分∠AGC;③∠FGA=37°;④∠MGK=18.5°.其中正确的结论是________.

答案： 答案 ①②③④
解析 $\because\angle EAD=\angle D$，$\angle B=\angle D$，$\therefore\angle EAD=\angle B$，
$\therefore AD// BC$，故①正确；
$\because AD// BC$，$\therefore\angle CKG=\angle AGK$，
$\because\angle CKG=\angle CGK$，
$\therefore\angle AGK=\angle CGK$，即$GK$平分$\angle AGC$，故②正确；
$\because\angle FGA$的余角比$\angle DGH$大$16^{\circ}$，
$\therefore90^{\circ}-\angle FGA=\angle DGH + 16^{\circ}$，
$\because\angle DGH=\angle FGA$，$\therefore90^{\circ}-\angle FGA=\angle FGA + 16^{\circ}$，
$\therefore\angle FGA = 37^{\circ}$，故③正确；
设$\angle AGM=\alpha$，$\angle MGK=\beta$，则$\angle AGK=\alpha+\beta$，
$\because GK$平分$\angle AGC$，$\therefore\angle CGK=\angle AGK=\alpha+\beta$，
$\because GM$平分$\angle FGC$，$\therefore\angle FGM=\angle CGM$，
即$\angle FGA+\angle AGM=\angle CGK+\angle MGK$，
$\therefore37^{\circ}+\alpha=\alpha+\beta+\beta$，解得$\beta = 18.5^{\circ}$，
即$\angle MGK = 18.5^{\circ}$，故④正确.

17.[答案含评分细则](2024山东庆云月考)(8分)计算:(M7208003)
(1)$\sqrt{(-4)^{2}}-\sqrt[3]{-8}+\sqrt{2\frac{1}{4}}+(-1)^{2023}$.
(2)$\sqrt{3}\times(3 - \sqrt{3})-\sqrt{2}\times(\sqrt{2}+\frac{1}{\sqrt{2}})$.

答案： 解析
(1)$\sqrt{(-4)^2}-\sqrt[3]{-8}+\sqrt{2\frac{1}{4}}+(-1)^{2023}$
$=4 + 2+\frac{3}{2}-1$ …………………………… 2分
$=\frac{13}{2}$. ……………………………………… 4分
(2)$\sqrt{3}\times(3-\sqrt{3})-\sqrt{2}\times(\sqrt{2}+\frac{1}{\sqrt{2}})$
$=3\sqrt{3}-3-2 - 1$ …………………………… 6分
$=3\sqrt{3}-6$. ………………………………… 8分