第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
1.(2024甘肃陇南武都二模)如图,直线a、b被直线c、d所截,若∠1 = 100°,∠2 = 80°,∠3 = 125°,则∠4的度数是(M7207006)
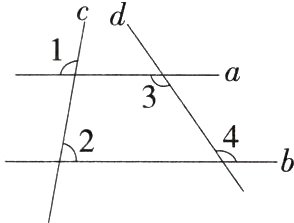
( )
A.55°
B.75°
C.100°
D.125°

( )
A.55°
B.75°
C.100°
D.125°
答案:
D $\because \angle 1 = 100^{\circ}, \angle 2 = 80^{\circ},$
$\therefore \angle 1 + \angle 2 = 180^{\circ}, \therefore a // b,$
$\therefore \angle 4 = \angle 3 = 125^{\circ}.$
故选D.
$\therefore \angle 1 + \angle 2 = 180^{\circ}, \therefore a // b,$
$\therefore \angle 4 = \angle 3 = 125^{\circ}.$
故选D.
2.(2024广东中考)如图,一把直尺、两个含30°角的三角尺拼接在一起,则∠ACE的度数为 ( )

A.120°
B.90°
C.60°
D.30°

A.120°
B.90°
C.60°
D.30°
答案:
C $\because \angle ABC = \angle ECD = 30^{\circ}, \therefore AB // CE,$
$\therefore \angle ACE = \angle A = 180^{\circ} - 90^{\circ} - 30^{\circ} = 60^{\circ}.$
故选C.
$\therefore \angle ACE = \angle A = 180^{\circ} - 90^{\circ} - 30^{\circ} = 60^{\circ}.$
故选C.
3.(2024湖南益阳二模)如图,∠B + ∠DCB = 180°,AC平分∠DAB,且∠D:∠DAC = 4:1,则∠D的度数是(M7207006)

( )
A.120°
B.110°
C.105°
D.100°

( )
A.120°
B.110°
C.105°
D.100°
答案:
A $\because \angle B + \angle DCB = 180^{\circ}, \therefore AB // CD,$
$\therefore \angle D + \angle DAB = 180^{\circ},$
设$\angle D = 4x^{\circ}$, 则$\angle DAC = x^{\circ},$
$\because AC$平分$\angle DAB,$
$\therefore \angle DAB = 2\angle DAC = 2x^{\circ},$
$\therefore 4x^{\circ} + 2x^{\circ} = 180^{\circ}, \therefore x = 30,$
$\therefore \angle D = 4x^{\circ} = 4 \times 30^{\circ} = 120^{\circ}.$ 故选A.
$\therefore \angle D + \angle DAB = 180^{\circ},$
设$\angle D = 4x^{\circ}$, 则$\angle DAC = x^{\circ},$
$\because AC$平分$\angle DAB,$
$\therefore \angle DAB = 2\angle DAC = 2x^{\circ},$
$\therefore 4x^{\circ} + 2x^{\circ} = 180^{\circ}, \therefore x = 30,$
$\therefore \angle D = 4x^{\circ} = 4 \times 30^{\circ} = 120^{\circ}.$ 故选A.
4.(2024云南曲靖二模)如图,a⊥c,b⊥c于点B,过点B的直线d交直线a于点A,若∠1 = 40°,则∠2的度数是(M7207006)

( )
A.50°
B.40°
C.30°
D.20°

( )
A.50°
B.40°
C.30°
D.20°
答案:
A 如图,

$\because \angle 1 = 40^{\circ}, \therefore \angle 3 = \angle 1 = 40^{\circ}.$
$\because a \perp c, b \perp c,$
$\therefore a // b, \angle 2 + \angle 4 = 90^{\circ},$
$\therefore \angle 4 = \angle 3 = 40^{\circ}.$
$\therefore \angle 2 = 90^{\circ} - \angle 4 = 90^{\circ} - 40^{\circ} = 50^{\circ}.$
故选A.
A 如图,

$\because \angle 1 = 40^{\circ}, \therefore \angle 3 = \angle 1 = 40^{\circ}.$
$\because a \perp c, b \perp c,$
$\therefore a // b, \angle 2 + \angle 4 = 90^{\circ},$
$\therefore \angle 4 = \angle 3 = 40^{\circ}.$
$\therefore \angle 2 = 90^{\circ} - \angle 4 = 90^{\circ} - 40^{\circ} = 50^{\circ}.$
故选A.
5.铅笔模型(2024浙江杭州上城期中)图1是某景区电动道闸门,将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,当CD平行于地面AE时,∠ABC + ∠BCD =(M7207006)



( )
A.180°
B.210°
C.250°
D.270°



( )
A.180°
B.210°
C.250°
D.270°
答案:
D 过点$B$作$BF // AE$, 如图,

$\because CD // AE, \therefore BF // CD,$
$\therefore \angle BCD + \angle CBF = 180^{\circ},$
$\because AB \perp AE, BF // AE, \therefore AB \perp BF, \therefore \angle ABF = 90^{\circ},$
$\therefore \angle ABC + \angle BCD = \angle ABF + \angle CBF + \angle BCD = 90^{\circ} + 180^{\circ} = 270^{\circ}.$
故选D.
模型解读
如果两条平行线中间有向外的拐点, 如图, 就得到了铅笔模型. 该模型常用结论: 若$AB // CD$, 则$\angle A + \angle AEC + \angle C = 360^{\circ}.$

D 过点$B$作$BF // AE$, 如图,

$\because CD // AE, \therefore BF // CD,$
$\therefore \angle BCD + \angle CBF = 180^{\circ},$
$\because AB \perp AE, BF // AE, \therefore AB \perp BF, \therefore \angle ABF = 90^{\circ},$
$\therefore \angle ABC + \angle BCD = \angle ABF + \angle CBF + \angle BCD = 90^{\circ} + 180^{\circ} = 270^{\circ}.$
故选D.
模型解读
如果两条平行线中间有向外的拐点, 如图, 就得到了铅笔模型. 该模型常用结论: 若$AB // CD$, 则$\angle A + \angle AEC + \angle C = 360^{\circ}.$

6.教材变式 如图,MN//BC,BD⊥DC,∠1 = ∠2 = 60°,DC是∠NDE的平分线.(M7207006)
(1)AB与DE平行吗?请说明理由.
(2)试说明∠ABC = ∠C.
(3)求∠ABD的度数.
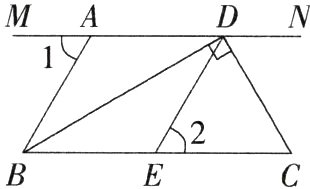
(1)AB与DE平行吗?请说明理由.
(2)试说明∠ABC = ∠C.
(3)求∠ABD的度数.

答案:
解析
(1)$AB // DE$. 理由:$\because MN // BC, \angle 1 = 60^{\circ},$
$\therefore \angle ABC = \angle 1 = 60^{\circ}. \because \angle 1 = \angle 2, \therefore \angle ABC = \angle 2.$
$\therefore AB // DE.$
(2)证明:$\because MN // BC, \therefore \angle NDE + \angle 2 = 180^{\circ}.$
$\therefore \angle NDE = 180^{\circ} - \angle 2 = 180^{\circ} - 60^{\circ} = 120^{\circ}.$
$\because DC$是$\angle NDE$的平分线,$\therefore \angle EDC = \angle NDC = \frac{1}{2} \angle NDE = 60^{\circ}. \because MN // BC, \therefore \angle C = \angle NDC = 60^{\circ}.$
$\because \angle ABC = 60^{\circ}, \therefore \angle ABC = \angle C.$
(3)$\because \angle ADC + \angle NDC = 180^{\circ}, \angle NDC = 60^{\circ},$
$\therefore \angle ADC = 180^{\circ} - \angle NDC = 180^{\circ} - 60^{\circ} = 120^{\circ}.$
$\because BD \perp DC, \therefore \angle BDC = 90^{\circ}.$
$\therefore \angle ADB = \angle ADC - \angle BDC = 120^{\circ} - 90^{\circ} = 30^{\circ}.$
$\because MN // BC, \therefore \angle DBC = \angle ADB = 30^{\circ}.$
$\because \angle ABC = 60^{\circ}, \therefore \angle ABD = 60^{\circ} - 30^{\circ} = 30^{\circ}.$
(1)$AB // DE$. 理由:$\because MN // BC, \angle 1 = 60^{\circ},$
$\therefore \angle ABC = \angle 1 = 60^{\circ}. \because \angle 1 = \angle 2, \therefore \angle ABC = \angle 2.$
$\therefore AB // DE.$
(2)证明:$\because MN // BC, \therefore \angle NDE + \angle 2 = 180^{\circ}.$
$\therefore \angle NDE = 180^{\circ} - \angle 2 = 180^{\circ} - 60^{\circ} = 120^{\circ}.$
$\because DC$是$\angle NDE$的平分线,$\therefore \angle EDC = \angle NDC = \frac{1}{2} \angle NDE = 60^{\circ}. \because MN // BC, \therefore \angle C = \angle NDC = 60^{\circ}.$
$\because \angle ABC = 60^{\circ}, \therefore \angle ABC = \angle C.$
(3)$\because \angle ADC + \angle NDC = 180^{\circ}, \angle NDC = 60^{\circ},$
$\therefore \angle ADC = 180^{\circ} - \angle NDC = 180^{\circ} - 60^{\circ} = 120^{\circ}.$
$\because BD \perp DC, \therefore \angle BDC = 90^{\circ}.$
$\therefore \angle ADB = \angle ADC - \angle BDC = 120^{\circ} - 90^{\circ} = 30^{\circ}.$
$\because MN // BC, \therefore \angle DBC = \angle ADB = 30^{\circ}.$
$\because \angle ABC = 60^{\circ}, \therefore \angle ABD = 60^{\circ} - 30^{\circ} = 30^{\circ}.$
查看更多完整答案,请扫码查看


