《2025年5年中考3年模拟七年级数学下册人教版》

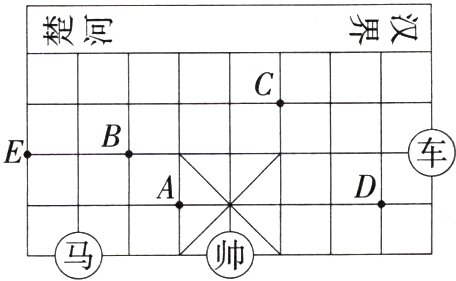
22. 情境题·中华优秀传统文化 （2024山西朔州期中）（8分）中国象棋棋盘由九条平行的竖线和十条平行的横线相交组成，共有九十个交叉点，棋子就摆在交叉点上. 如图所示的是中国象棋棋盘的一部分，按照象棋规则，棋子“马”只能沿“日”形的对角线走. 例如：图中“马”只能由其所在的位置一步走到点A或点B或点E处.（M7209003）
(1)如果“帅”位于点(0，0)，“车”位于点(4，2)，那么“马”所在的点的坐标为________，点C的坐标为________，点D的坐标为________.
(2)若“帅”位于点(0，0)，“马”的位置在C点，则为了让“马”到达D点，请写出一种你认为合理的行走路线(用坐标表示).

答案：
22解析　
(1)以“帅”位于点(0,0)画出坐标系如图,则“马”所在的点的坐标为(−3,0),点C的坐标为(1,3),点D的坐标为(3,1).

(2)若“马”的位置在C点，则为了到达D点，所走路线可以为C(1,3)→(2,1)→(3,3)→(1,2)→D(3,1)(答案不唯一).

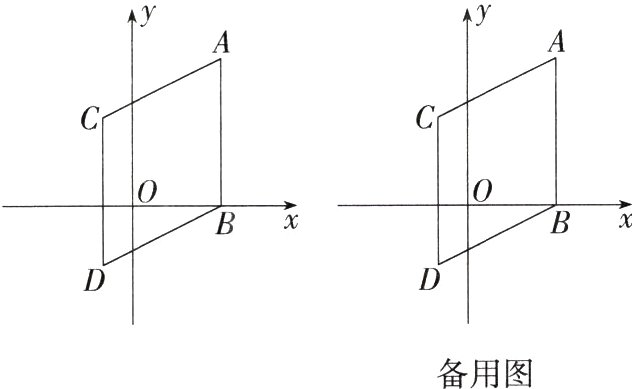
23.（12分）如图，在平面直角坐标系中，点A，B的坐标分别为(3，5)，(3，0). 将线段AB向下平移2个单位长度，再向左平移4个单位长度，得到线段CD，连接AC，BD.
(1)直接写出点C、D的坐标.
(2)M，N分别是线段AB，CD上的动点，点M从点A出发向点B运动，速度为每秒1个单位长度，点N从点D出发向点C运动，速度为每秒0.5个单位长度，若两点同时出发，则几秒后MN//x轴?
(3)若∠CAB = α，设点P是x轴上一动点(不与点B重合)，则∠ACP与∠CPB存在怎样的数量关系?

答案：
23解析　
(1)C(−1,3),D(−1,−2).
(2)设t秒后MN//x轴,则有5−t=0.5t−2,
解得$t=\frac{14}{3}，$
∴$\frac{14}{3}$秒后MN//x轴.
(3)根据题意可知AB⊥x轴.
①如图1,延长AC交x轴于E,当点P在直线AC的左侧时,易证∠ACP=∠CPE+∠PEC=∠CPE+∠EAB+∠ABE,
∴∠ACP=∠CPB+90°+α.

②当点P在直线AC上时,∠ACP=180°,∠CPB=180°−90°−α=90°−α,则∠ACP=∠CPB+90°+α.
③如图2,当点P在直线AC的右侧且在直线AB的左侧时,∠ACP+∠CPB=360°−∠CAB−∠ABP=270°−α.

④如图3,当点P在直线AB的右侧时,
∵∠AMC=∠BMP,
∴∠ACP+∠CAB=∠ABP+∠CPB,
∴∠ACP =∠CPB+90°−α.
综上所述,∠ACP与∠CPB的数量关系为∠ACP=∠CPB+90°+α或∠ACP+∠CPB=270°−α或∠ACP =∠CPB+90°−α.