《2025年5年中考3年模拟七年级数学下册人教版》

11.(2024安徽阜阳期末,4,★☆☆)若1 - m ＜ 1 - n,则下列不等式一定成立的是(M7211001) ( )
A.-2m + 1 ＞ -2n + 1
B.m + 14 ＞ n + 14
C.m + a ＞ n + b
D.-am ＞ -an

答案： 11B 1−m＜1−n，不等式两边都减1，得−m＜−n，不等式两边都乘−1，得m＞n。
A.m＞n，不等式两边都乘−2，得−2m＜−2n，不等式两边都加1，得−2m+1＜−2n+1，故选项A错误；
B.m＞n，不等式两边都加14，得m+14＞n+14，故选项B正确；
C.m＞n，不等式左边加a，右边加b，不确定a和b是否相等，所以m+a＞n+b不一定成立，故C错误；
D.m＞n，不能确定−a与0的关系，所以−am＞−an不一定成立，故D选项错误。故选B。

12.(2024山东烟台中考,4,★☆☆)实数a,b,c在数轴上的位置如图所示,下列结论正确的是 ( )

答案： 12B 由数轴可得−3＜a＜−2，−2＜b＜−1，3＜c＜4，
∴b+c＜3，故A选项中结论错误；
∵a＜0，c＞0，
∴a−c＜0，故B选项中结论正确；
∵|a|＜3，|c|＞3，
∴|a|＜|c|，故C选项中结论错误；
∵a＜b，
∴−2a＞−2b，故D选项中结论错误。故选B。

13.易错题 (2023安徽合肥瑶海期末,8,★☆☆)已知不等式$\frac{x - 3}{2}＜1$的解都是关于x的不等式x ＜ a的解,则a的取值范围是(M7211001) ( )
A.a ＞ 5
B.a ≥ 5
C.a ＜ 5
D.a ≤ 5

答案： 13B 不等式$\frac{x−3}{2}$＜1两边同乘2，得x−3＜2，
两边同加3，得x＜2+3，即x＜5。
∵不等式$\frac{x−3}{2}$＜1的解都是关于x的不等式x＜a的解，
∴a≥5，故选B。
易错警示
在判断取值范围的端点值是否可以取到时，易出错。

14.(2023北京朝阳期末,19,★☆☆)解不等式5x + 3 ≥ 3x - 1,并在数轴上表示该不等式的解集.(M7211001)

答案：
解析 不等式两边同时减3，得5x≥3x−4。
不等式两边同时减3x，得2x≥−4。
不等式两边同除以2，得x≥−2。
不等式的解集在数轴上表示如图：

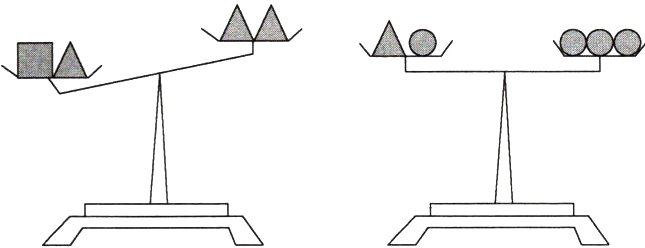
15.几何直观 用“▲”“●”“■”分别表示三种不同的物体,现用天平称重两次,情况如图所示,那么▲,●,■这三种物体按质量从大到小排列应为 ( )

A.■,●,▲
B.▲,■,●
C.■,▲,●
D.●,▲,■

答案：
15C 设 的质量分别为a,b,c，
由第一架天平得a+c＞2a，
不等式两边都减去a，得c＞a；
由第二架天平得a+b=3b，
方程两边都减去b，得a=2b，
故c＞a＞b。故选C。

16.运算能力 新考向·新定义试题 对于两个关于x的不等式,若有且仅有一个整数使得这两个不等式同时成立,则称这两个不等式是“共联”的,这个整数称为“联点”.例如,不等式x ＞ 1和不等式x ＜ 3是“共联”的,联点为2.(M7211001)
(1)不等式x - 1 ＜ 2和x - 2 ≥ 0是“共联”的,联点为________.
(2)若关于x的不等式x - a ＜ 0和x ＞ 0是“共联”的,则a的最大值为________.

答案： 解析
(1)x−1＜2，不等式两边都加1，得x＜3。
x−2≥0，不等式两边都加2，得x≥2，
∵不等式x−1＜2和x−2≥0是“共联”的，有且仅有x =2使得这两个不等式同时成立，
∴联点为2。
(2)x−a＜0，不等式两边都加a，得x＜a。
∵x−a＜0和x＞0是“共联”的，
∴1＜a≤2。
∴a的最大值为2。