《2025年5年中考3年模拟七年级数学下册人教版》

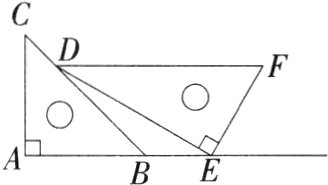
10.(2024四川凉山州中考,4,)一副直角三角尺按如图所示的方式摆放，点E在AB的延长线上，当DF//AB时，∠EDB的度数为(M7207006) ( )

A.10°
B.15°
C.30°
D.45°

答案： B
∵DF//AB，
∴∠FDB = ∠ABC = 45°，
∴∠EDB = ∠FDB - ∠EDF = 45° - 30° = 15°，故选B.

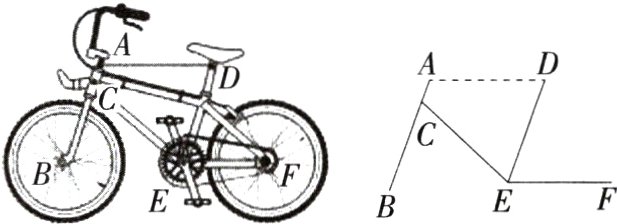
11.情境题·共享单车(2024浙江舟山定海三模改编,4,)骑共享单车这种“低碳”出行方式已融入我们的日常生活.如图所示的是共享单车车架的示意图.已知AB//DE，∠BCE = 67°，∠CEF = 137°，若AD//EF，则∠ADE的度数为(M7207006) ( )

A.43°
B.53°
C.70°
D.67°

答案： C
∵AB//DE，
∴∠BCE = ∠CED = 67°，
∵∠CEF = 137°，
∴∠DEF = ∠CEF - ∠CED = 70°，
∵AD//EF，
∴∠ADE = ∠DEF = 70°. 故选C.

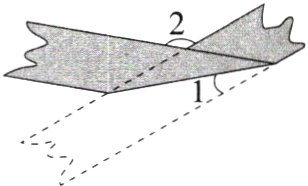
12.(2023浙江台州中考,13,)用一张等宽的纸条折成如图所示的图案，若∠1 = 20°，则∠2的度数为________.(M7207006)

答案：
答案 140°
解析 如图，

由折叠可得∠ACD = 2∠1 = 40°.
∵AB//CD，
∴∠BAC + ∠ACD = 180°.
∴∠BAC = 180° - 40° = 140°.
∴∠2 = ∠BAC = 140°.

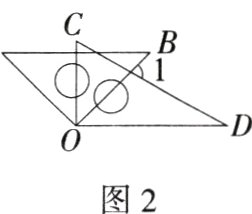
13.(2024山东滨州中考,12,)一副三角尺如图1摆放，把三角尺AOB绕公共顶点O顺时针旋转至图2，即AB//OD时，∠1的大小为________°。

答案：
答案 75
解析 如图，因为AB//OD，所以∠BOD = ∠B = 45°，
又因为∠D = 30°，所以∠2 = 180° - 30° - 45° = 105°，
所以∠1 = 180° - ∠2 = 75°.

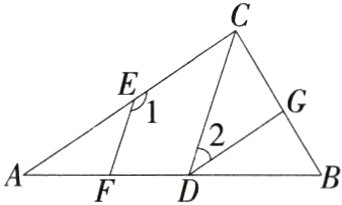
14.(2024福建龙岩八中月考,23,)已知：如图，EF//CD，GD//CA.(M7207006)
(1)求证：∠1 + ∠2 = 180°.
(2)若CD平分∠ACB，DG平分∠CDB，且∠A = 40°，求∠ACB的度数.

答案： 解析
(1) 证明：
∵EF//CD，
∴∠1 + ∠ECD = 180°，
∵GD//AC，
∴∠2 = ∠ECD，
∴∠1 + ∠2 = 180°.
(2)
∵GD//AC，
∴∠GDB = ∠A = 40°，∠ACD = ∠2.
∵DG平分∠CDB，
∴∠2 = ∠BDG = 40°.
∴∠ACD = ∠2 = 40°.
∵CD平分∠ACB，
∴∠ACB = 2∠ACD = 80°.

15.应用意识·跨地理·地球周长 埃拉托色尼是古希腊著名的地理学家，他曾巧妙地估算出地球的周长(这里的周长通常指的是赤道周长).如图，A处是塞尼城中的一口深井，夏至日中午12时，太阳光可直射井底.B处为亚历山大城，它与塞尼城几乎在一条经线上，两地距离d约为800 km，于是地球周长可近似表示为$\frac{360°}{\theta}×d km，$太阳光线可看作平行线，埃拉托色尼在亚历山大城测得天顶方向与太阳光线的夹角α = 7.2°.根据α可以推出θ的大小，依据是________________；埃拉托色尼估算的地球周长为________km.

答案： 答案 两直线平行，同位角相等；40 000
解析 因为太阳光线可看作平行线，则θ = α = 7.2°(两直线平行，同位角相等). 因为亚历山大城、塞尼城之间的距离约为800 km，所以地球周长约为$\frac{360^{\circ}}{7.2^{\circ}}\times 800 = 40000(km)$.