《2025年5年中考3年模拟七年级数学下册人教版》

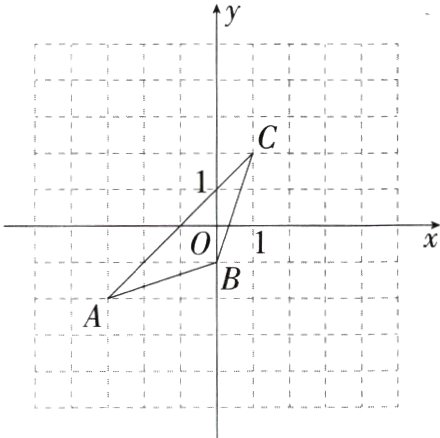
23.[答案含评分细则](2024河北邢台期中)(8分)三角形ABC在平面直角坐标系中的位置如图所示.(M7209002)
(1)分别写出点A,B,C的坐标,并求三角形ABC的面积.
(2)过点(−4,−4)作直线l//x轴,若点P在直线l上运动,连接AP,当线段AP长度最小时,直接写出此时点P的坐标.
(3)若点Q在y轴上,且三角形BCQ与三角形ABC的面积相等,求点Q的坐标.

答案：
解析
(1)$A(-3,-2)$，$B(0,-1)$，$C(1,2)$，$\triangle ABC$的面积为$4\times4-\frac{1}{2}\times4\times4-\frac{1}{2}\times3\times1-\frac{1}{2}\times(1 + 4)\times1 = 4$.
(2)如图所示，线段$AP$长度最小时，$AP\perp l$，
此时$P$的坐标为$(-3,-4)$. ………………… 5分

(3)设点$Q$的坐标为$(0,m)$，
$\therefore BQ=\vert m + 1\vert$， …………………………… 6分
$\therefore\triangle BCQ$的面积为$\frac{1}{2}\times\vert m + 1\vert\times1 = 4$，
解得$m = 7$或$-9$，
$\therefore$点$Q$的坐标为$(0,7)$或$(0,-9)$. …………… 8分

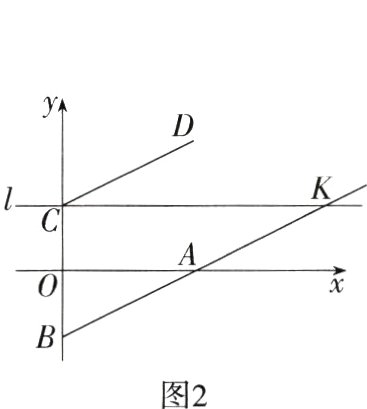
24.[答案含评分细则](10分)在平面直角坐标系中,有点A(6,0),B(0,−3),将线段AB向上平移k个单位得到线段DC.(M7207006)
(1)如图1,点E为线段CD上任意一点,点F 为线段AB上任意一点,∠EOF=135°.点G 为线段AB与线段CD之间一点,连接GE,GF,∠DEG=$\frac{1}{3}$∠DEO,∠AFG=$\frac{1}{3}$∠AFO,求∠EGF的度数.
(2)如图2,当k=6时,过点C作直线l//x轴,延长BA交l于K;
①求K点的坐标;
②若点M为直线l上一点,M不与K重合,△MAB的面积为10,求点M的坐标.
　

答案：
解析
(1)由平移可知$CD// AB$，设$\angle AFG=y^{\circ}$，$\angle DEG=x^{\circ}$，则$\angle AFO = 3y^{\circ}$，$\angle DEO = 3x^{\circ}$，
如图，过$O$作$OP// CD$，则$OP// CD// AB$，
$\therefore\angle AFO+\angle FOP = 180^{\circ}$，$\angle DEO+\angle EOP = 180^{\circ}$，
$\therefore\angle DEO+\angle AFO+\angle EOP+\angle FOP = 360^{\circ}$，
即$3x^{\circ}+3y^{\circ}+135^{\circ}=360^{\circ}$，$\therefore x^{\circ}+y^{\circ}=75^{\circ}$， ……… 2分
过$G$作$GH// CD$，则$GH// CD// AB$，
$\therefore\angle HGF=\angle AFG=y^{\circ}$，$\angle EGH=\angle DEG=x^{\circ}$， … 4分
$\therefore\angle EGF=\angle EGH+\angle HGF=x^{\circ}+y^{\circ}=75^{\circ}$. ……… 5分

(2)①如图，连接$AC$，
$\because k = 6$，$\therefore D(6,6)$，$C(0,3)$，
设$K(n,3)$，
$\because S_{\triangle BCK}=S_{\triangle ABC}+S_{\triangle ACK}$，
$\therefore\frac{1}{2}\times6\times n=\frac{1}{2}\times6\times6+\frac{1}{2}\times3\times n$，
解得$n = 12$，
$\therefore K$点的坐标为$(12,3)$. ………………… 7分

②如图，设$M(m,3)$，
$\because S_{\triangle MAB}=S_{\triangle MKB}-S_{\triangle MKA}=10$，
$\therefore\frac{1}{2}\times\vert m - 12\vert\times6-\frac{1}{2}\times\vert m - 12\vert\times3 = 10$， ……… 8分
解得$m=\frac{16}{3}$或$m=\frac{56}{3}$， ………………… 9分
$\therefore M$的坐标为$(\frac{16}{3},3)$或$(\frac{56}{3},3)$. …………… 10分