《2025年5年中考3年模拟七年级数学下册人教版》

1.(2024北京中考)如图,直线AB和CD相交于点O,OE⊥OC.若∠AOC=58°,则∠EOB的大小为（ ）

A.29°
B.32°
C.45°
D.58°

答案： B $\because OE\perp OC$，$\therefore \angle COE = 90^{\circ}$，
$\because \angle AOC + \angle COE + \angle EOB = 180^{\circ}$，$\angle AOC = 58^{\circ}$，
$\therefore \angle EOB = 180^{\circ} - 90^{\circ} - 58^{\circ} = 32^{\circ}$.
故选B.

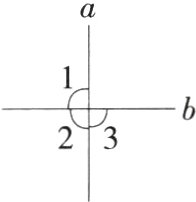
2.新独家原创 已知直线a、b相交,如图所示,添加下列条件:①∠1 = 90°;②∠1 + ∠2 = 180°;③∠1 = ∠3;④∠1 + ∠3 = 180°;⑤∠1 = ∠2 = ∠3.其中能得到a⊥b的有（ ）

A.1个
B.2个
C.3个
D.4个

答案： 2 C ①因为$\angle 1 = 90^{\circ}$，所以$a\perp b$；
②由$\angle 1 + \angle 2 = 180^{\circ}$，不能推出$a\perp b$；
③由$\angle 1 = \angle 3$，不能推出$a\perp b$；
④因为$\angle 1 = \angle 3$，$\angle 1 + \angle 3 = 180^{\circ}$，所以$\angle 1 = 90^{\circ}$，所以$a\perp b$；
⑤设$\angle 2$的对顶角为$\angle 4$，所以$\angle 2 = \angle 4$.
因为$\angle 1 = \angle 2 = \angle 3$，所以$\angle 1 = \angle 2 = \angle 3 = \angle 4$.
因为$\angle 1 + \angle 2 + \angle 3 + \angle 4 = 360^{\circ}$，所以$\angle 1 = 90^{\circ}$，所以$a\perp b$.
综上，能得到$a\perp b$的条件为①④⑤，共3个，故选C.

3.新考法(2024河北威县月考)利用三角尺或量角器判断,图中的两点所成的直线能与直线l垂直的是（ ）

A.点M和点N
B.点P和点Q
C.点M和点Q
D.点N和点P

答案：
3 C 本题需要学生动手连线，测量角的度数来判断两直线是否垂直.既考查了垂直的定义，又考查了学生的动手能力，考法新颖.
按选项A、B、C、D的顺序作直线$MN$，$PQ$，$MQ$（交$l$于$A$），$NP$（交$l$于$B$），如图所示：

利用三角尺可得出$MQ\perp$直线$l$（或利用量角器量出$\angle QAC$（或$\angle QAB$），$\angle PBD$（或$\angle PBC$）的度数即可得出$MQ\perp$直线$l$）.
故选C.

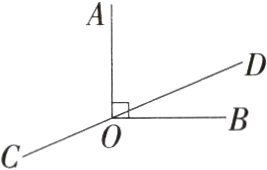
4.教材变式(2024河南商丘一中模拟)如图,点O在直线CD上,OA⊥OB于点O,若∠AOD = 3∠BOD,则∠AOC的度数为（ ）

A.105°
B.125°
C.110.5°
D.112.5°

答案： 4 D 因为$OA\perp OB$于点$O$，所以$\angle AOB = 90^{\circ}$，
因为$\angle AOD = 3\angle BOD$，所以$\angle AOB = 4\angle BOD$，
所以$\angle BOD = 22.5^{\circ}$，所以$\angle AOD = 67.5^{\circ}$，
所以$\angle AOC = 180^{\circ} - 67.5^{\circ} = 112.5^{\circ}$.故选D.

5.(2024广东佛山南海期中)如图,CO⊥AB于点O,DE经过点O,∠COD = 50°,则∠AOE的度数为________.(M7207002)

答案： 答案 $40^{\circ}$
解析 因为$CO\perp AB$，
所以$\angle AOC = 90^{\circ}$，
因为$\angle COD = 50^{\circ}$，
所以$\angle AOE = 180^{\circ} - \angle AOC - \angle COD = 40^{\circ}$.

6.(2024江苏泗洪期末)如图,OC⊥AB交直线AB于点O,射线OD、OE在∠BOC内,OE平分∠BOD,其中∠COD = 32°.(M7207002)
(1)求∠BOD的度数.
(2)求∠AOE的度数.

答案： 解析 （1）因为$OC\perp AB$，所以$\angle BOC = 90^{\circ}$，
因为$\angle COD = 32^{\circ}$，所以$\angle BOD = \angle BOC - \angle COD = 90^{\circ} - 32^{\circ} = 58^{\circ}$.
（2）因为$\angle BOD = 58^{\circ}$，$OE$平分$\angle BOD$，
所以$\angle BOE = \frac{1}{2}\angle BOD = 29^{\circ}$，
所以$\angle AOE = 180^{\circ} - \angle BOE = 180^{\circ} - 29^{\circ} = 151^{\circ}$.

7.过点P向线段AB所在直线引垂线,正确的画法是（ ）

A. B. C. D.

答案： 7 C A选项中$PB$与$AB$不垂直；B选项中所作垂线没有过点$P$；C选项符合过点$P$作线段$AB$所在直线的垂线的要求；D选项中$PO$是一条线段，不是一条直线.

8.(2024江西大余月考)过直线m外的一点Q作m的垂线,下列借助直角三角尺的操作正确的是（ ）

A. B. C. D.

答案： 8 D 根据垂线的作法，将直角三角尺的一条直角边落在直线$m$上，另一条直角边过点$Q$后沿该直角边作直线即可.