《2025年5年中考3年模拟七年级数学下册人教版》

18.[推理能力](2024广东广州天河月考)如图，已知直线AB和CD相交于点O(∠BOD为锐角)，点E在直线AB上方，∠EOB = 90°，OF平分∠BOD.(M7207001)
(1)如图1，若∠BOF = 40°，求∠COE的度数.
(2)如图2，∠DOF + $\frac{1}{2}$∠COE = ________°.
(3)[易错题]若∠COE : ∠EOF = 4 : 25，过点O作射线OG，使∠GOF = $\frac{2}{5}$∠AOD，求∠BOG的度数.

答案： 解析
(1) 因为 OF 平分∠BOD，∠BOF = 40°，
所以∠DOF = ∠BOF = 40°，
因为∠EOB = 90°，
所以∠COE = 180° - ∠DOF - ∠BOF - ∠EOB = 180° - 40° - 40° - 90° = 10°.
(2) 因为∠EOB = 90°，所以∠BOD + ∠COE = 180° - ∠BOE = 180° - 90° = 90°，
又因为$∠DOF = \frac{1}{2}∠BOD，$
所以$∠DOF + \frac{1}{2}∠COE = \frac{1}{2}(∠BOD + ∠COE) = \frac{1}{2}×90° = 45°.$故答案为 45.
(3) 设∠FOD = α，
因为 OF 平分∠BOD，所以∠BOF = ∠FOD = α，
因为∠EOB = 90°，所以∠COE = 180° - ∠FOD - ∠BOF - ∠EOB = 90° - 2α，∠EOF = ∠EOB + ∠BOF = 90° + α，
因为∠COE : ∠EOF = 4 : 25，
即(90° - 2α) : (90° + α) = 4 : 25，
所以 4(90° + α) = 25(90° - 2α)，
解得α = 35°，所以∠BOD = 2∠BOF = 2α = 70°，
所以∠AOD = 180° - ∠BOD = 180° - 70° = 110°，
所以$∠GOF = \frac{2}{5}∠AOD = \frac{2}{5}×110° = 44°，$
当射线 OG 与射线 OB 在 OF 异侧时，
∠BOG = ∠GOF + ∠BOF = 44° + 35° = 79°，
当射线 OG 与射线 OB 在 OF 同侧时，
∠BOG = ∠GOF - ∠BOF = 44° - 35° = 9°.
综上，∠BOG 的度数是 79°或 9°.
易错警示
因为没有说 OG 的位置，所以 OG 可能与射线 OB 在 OF 的同侧，也有可能与射线 OB 在 OF 的异侧，本题容易只讨论其中的一种情况，而漏掉另一种情况. 谨记：无图有陷阱.

19.[推理能力]观察图形，寻找对顶角和邻补角.

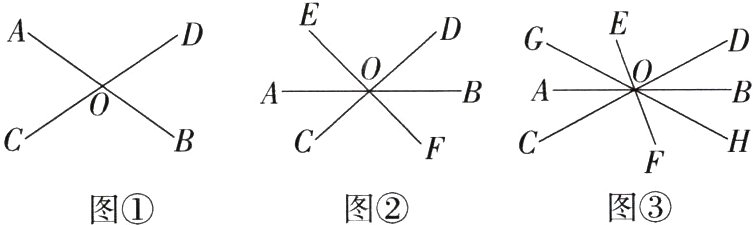
(1)如图①，共有________对对顶角，________对邻补角.
(2)如图②，共有________对对顶角，________对邻补角.
(3)如图③，共有________对对顶角，________对邻补角.
(4)探究：若n条直线相交于一点，则可形成多少对对顶角？多少对邻补角？
(5)根据探究结果，试求2025条直线相交于一点时，所形成的对顶角、邻补角的对数.

答案： 解析
(1) 共有 1×2 = 2 对对顶角，2×(1×2) = 4 对邻补角. 故填 2；4.
(2) 共有 2×3 = 6 对对顶角，2×(2×3) = 12 对邻补角. 故填 6；12.
(3) 共有 3×4 = 12 对对顶角，2×(3×4) = 24 对邻补角. 故填 12；24.
(4) 若 n 条直线相交于一点，则可形成 n(n - 1) 对对顶角，2n(n - 1) 对邻补角.
(5) 2025 条直线相交于一点时，可形成(2025 - 1)×2025 = 4098600 对对顶角，2×(2025 - 1)×2025 = 8197200 对邻补角.