《2025年5年中考3年模拟七年级数学下册人教版》

8.教材变式 在括号内填上理由.
如图，直线NF与直线HB，CD分别交于点E，F，直线AM与直线HB交于点A，且∠1 = ∠4 = 105°，∠2 = 75°.试说明AM//NF，AB//CD.

证明：∵ ∠2 = ∠3( )，∠2 = 75°(已知)，
∴ ∠3 = 75°.
∵ ∠1 = 105°(已知)，
∴ ∠MAB = 180° - ∠1 = 75°，∴ ∠MAB = ∠3.
∴ AM//NF( ).
∵ ∠3 = 75°，∠4 = 105°，
∴ ∠3 + ∠4 = 180°，
∴ AB//CD( ).

答案： 答案 对顶角相等；内错角相等，两直线平行；同旁内角互补，两直线平行

9.新独家原创 如图，已知BE，CF分别是∠ABC和∠BCD的三等分线(∠ABE ＜ ∠EBC，∠DCF ＜ ∠BCF).(M7207005)
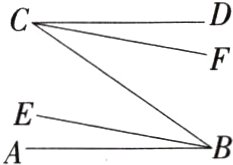
(1)若∠BCD = ∠ABC，试判断BE和CF的位置关系，并说明理由.
(2)若∠ABE = ∠DCF，试判断AB和CD的位置关系，并说明理由.

答案： 解析
(1)BE//CF. 理由如下：
∵BE，CF 分别是∠ABC 和∠BCD 的三等分线，∠ABE ＜ ∠EBC，∠DCF ＜ ∠BCF，
∴$∠CBE = \frac{2}{3}∠ABC，$$∠BCF = \frac{2}{3}∠BCD.$
∵∠BCD = ∠ABC，
∴∠CBE = ∠BCF.
∴BE//CF.
(2)AB//CD. 理由如下：
∵BE，CF 分别是∠ABC 和∠BCD 的三等分线，∠ABE ＜ ∠EBC，∠DCF ＜ ∠BCF，
∴∠ABC = 3∠ABE，∠BCD = 3∠DCF.
∵∠ABE = ∠DCF，
∴∠ABC = ∠BCD.
∴AB//CD.

10.一题多解 如图所示，∠BAF = 38°，DC⊥CE，∠ACE = 128°.试判断直线AB与DC的位置关系，并说明理由.

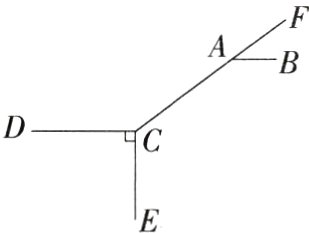
答案：
解析 【解法一】AB//DC. 理由如下：
因为∠BAF = 38°，∠BAF + ∠CAB = 180°，
所以∠CAB = 142°.
因为DC⊥CE，所以∠DCE = 90°.
又因为∠DCE + ∠ACE + ∠DCA = 360°，∠ACE = 128°，
所以∠DCA = 142°. 所以∠DCA = ∠CAB，
所以AB//DC(内错角相等，两直线平行).
【解法二】AB//DC. 理由如下：
如图，延长DC至G.
因为DC⊥CE，所以∠ECG = 90°，
因为∠ACG + ∠ECG = ∠ACE = 128°，
所以∠ACG = 38°.
所以∠BAF = ∠ACG，
所以AB//DC(同位角相等，两直线平行).
　　　　　　　

11.(2023山东临沂中考，5，★☆☆)在同一平面内，过直线l外一点P作l的垂线m，再过P作m的垂线n，则直线l与n的位置关系是 ( )
A.相交
B.相交且垂直
C.平行
D.不能确定

答案： C
∵l⊥m，n⊥m，
∴l//n(在同一平面内，垂直于同一条直线的两条直线平行). 故选C.

12.(2024河南禹州期中改编，15，★★☆)某舞台上的灯光由灯带上位于点A处和点C处的两盏激光灯控制.如图，光线AB与灯带AC的夹角∠A = 42°，当光线CB'与灯带AC的夹角∠ACB'的度数是________时，CB'//AB.(M7207005)

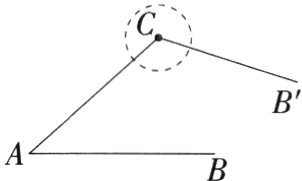
答案： 答案 138°或 42°
解析 当∠ACB'和∠A 是同旁内角，且∠ACB'+∠A = 180°时，CB'//AB，此时∠ACB' = 180° - ∠A = 180° - 42° = 138°.
当∠ACB'和∠A 是内错角，且∠ACB' = ∠A 时，CB'//AB，此时∠ACB' = ∠A = 42°.
综上，∠ACB'的度数是138°或42°时，CB'//AB.

13.(2024湖北襄阳月考，18，★★☆)如图，点E，F分别在AB，CD上，∠1 + ∠A = 90°，∠1 = ∠C，∠A与∠2互余，试说明CE//BF.(M7207005)

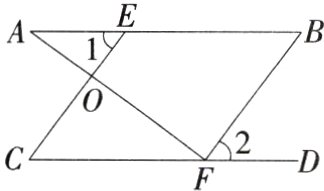
答案： 证明
∵∠1 + ∠A = 90°，∠A 与∠2 互余，
∴∠1 = ∠2.
∵∠1 = ∠C，
∴∠C = ∠2，
∴CE//BF.