《2025年5年中考3年模拟七年级数学下册人教版》

1.(2023浙江嘉兴中考)-8的立方根是 ( )
A.-2
B.2
C.±2
D.不存在

答案： A $\because (-2)^3 = -8$，$\therefore -8$的立方根是$-2$，故选A.

2.(2024天津期中)若一个数的立方根为-$\frac{1}{3}$，则这个数为(M7208001) ( )
A.-$\frac{1}{9}$
B.$\frac{1}{9}$
C.-$\frac{1}{27}$
D.$\frac{1}{27}$

答案： C $\because (-\frac{1}{3})^3 = -\frac{1}{27}$，$\therefore -\frac{1}{27}$的立方根为$-\frac{1}{3}$，故选C.

3.下列说法正确的是 ( )
A.±3是27的立方根
B.4的立方根是2
C.0.01的立方根是0.1
D.-125的立方根是-5

答案： D A.3是27的立方根，故A选项错误；
B.4的立方根是$\sqrt[3]{4}$，故B选项错误；
C.0.1是0.001的立方根，故C选项错误；
D.-125的立方根为-5，故D选项正确. 故选D.

4.新独家原创 王老师将一个小西瓜放在一个透明的正方体的盒子里，成熟时长成了一个体积为27000 cm³的正方体西瓜。这个正方体西瓜的棱长是________cm。

答案： 答案 30
解析 这个正方体西瓜的棱长为$\sqrt[3]{27000}=30$ cm.

5.求下列各数的立方根:(M7208001)
(1)216. (2) - 0.125. (3)$\frac{8}{343}$. (4)-$\frac{64}{125}$.

答案： 解析
(1)$\because 6^3 = 216$，$\therefore 216$的立方根是6.
(2)$\because (-0.5)^3 = -0.125$，
$\therefore -0.125$的立方根是-0.5.
(3)$\because (\frac{2}{7})^3 = \frac{8}{343}$，$\therefore \frac{8}{343}$的立方根是$\frac{2}{7}$.
(4)$\because (-\frac{4}{5})^3 = -\frac{64}{125}$，$\therefore -\frac{64}{125}$的立方根是$-\frac{4}{5}$.

6.求下列各式的值：
(1)$\sqrt[3]{-27}$. (2)$\sqrt[3]{2\frac{10}{27}}$. (3)$\sqrt[3]{-\frac{1}{1000}}$.

答案： 解析
(1)$\sqrt[3]{-27}$表示-27的立方根，是-3，
即$\sqrt[3]{-27} = -3$.
(2)$\sqrt[3]{2\frac{10}{27}}$表示$\frac{64}{27}$的立方根，是$\frac{4}{3}$，即$\sqrt[3]{\frac{64}{27}} = \frac{4}{3}$.
(3)$\sqrt[3]{-\frac{1}{1000}}$表示$-\frac{1}{1000}$的立方根，是$-\frac{1}{10}$，
即$\sqrt[3]{-\frac{1}{1000}} = -\frac{1}{10}$.

7.求下列各式中x的值：
(1)3x³ - 1 = 23. (2)(x - 1)³ - 2 = 7.

答案： 解析
(1)移项、合并同类项，得$3x^3 = 24$，
系数化为1，得$x^3 = 8$，
开立方，得$x = 2$.
(2)移项、合并同类项，得$(x - 1)^3 = 9$，
开立方，得$x - 1 = \sqrt[3]{9}$，
解得$x = 1+\sqrt[3]{9}$.

8.下列命题正确的是 ( )
A.正数有两个立方根
B.一个数的立方根不是正数就是负数
C.负数没有立方根
D.一个不为零的数的立方根和这个数同号，0的立方根是0

答案： D 正数只有一个立方根，故A错；0的立方根是0，故B错；负数有立方根，故C错. 故选D.

9.下列式子不正确的是 ( )
A.$\sqrt[3]{-a}=-\sqrt[3]{a}$
B.$\sqrt[3]{a³}=a$
C.($\sqrt[3]{a}$)³ = a
D.(-$\sqrt[3]{a}$)³ = a

答案： D 由立方根的性质知$(-\sqrt[3]{a})^3 = -a$，故选项D中的式子不正确，符合题意. 故选D.

10.(2024上海徐汇期末)计算:$\sqrt[3]{a}+\sqrt[3]{-a}$=________. (M7208001)

答案： 答案 0
解析 原式$=\sqrt[3]{a}-\sqrt[3]{a}=0$.

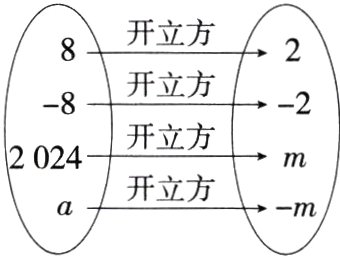
11.(2024福建三明三元期末)根据图中呈现的开立方运算关系，可以得出a的值为________. (M7208001)

答案： 答案 -2024
解析 根据题意得$m = \sqrt[3]{2024}$，
则$a = (-m)^3 = -m^3 = -(\sqrt[3]{2024})^3 = -2024$.

12.已知a的立方根是$\frac{5}{9}$，则 - a的立方根是________.

答案： 答案 $-\frac{5}{9}$
解析 由立方根的性质知，两个互为相反数的数的立方根也互为相反数，所以-a的立方根是$-\frac{5}{9}$.

13.(2024湖南长沙月考)已知$\sqrt[3]{2.37}≈1.333$，$\sqrt[3]{23.7}≈2.872$，那么$\sqrt[3]{2370}$约等于(M7208001) ( )
A.28.2
B.13.33
C.0.2872
D.0.1333

答案： B $\because \sqrt[3]{2.37} \approx 1.333$，2.37的小数点向右移动三位，是2370，$\therefore \sqrt[3]{2370} \approx 13.33$，故选B.