《2025年5年中考3年模拟七年级数学下册人教版》

17. （2024甘肃清水三模）如图，将直角三角形ABC沿着AB方向平移得到三角形DEF，若AB = 6 cm，BC = 4 cm，CH = 1 cm，图中阴影部分的面积为$\frac{21}{4}$cm²，则三角形ABC沿着AB方向平移的距离为________cm.（M7207008）
　　　　　　

答案： 答案 $\frac{3}{2}$
解析 由平移的性质可知，AD=BE，EF=BC=4 cm，$S_{\triangle ABC}=S_{\triangle DEF}$，
∴$S_{阴影部分}+S_{\triangle DBH}=S_{\triangle DBH}+S_{梯形BEFH}$，
∴$S_{梯形BEFH}=S_{阴影部分}=\frac{21}{4} cm^{2}$，
∵$S_{梯形BEFH}=\frac{1}{2}(BH + EF)\cdot BE$，
∴$\frac{1}{2}\times(4 - 1 + 4)\cdot BE=\frac{21}{4}$，解得$BE=\frac{3}{2} cm$，
∴三角形ABC沿着AB方向平移的距离为$\frac{3}{2} cm$.

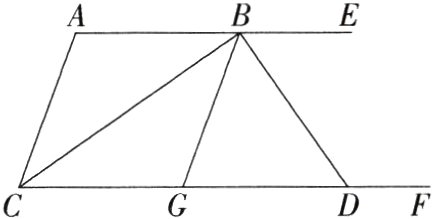
18. 如图，AE//CF，∠ACF的平分线交AE于点B，G是CF上的一点，∠EBG的平分线交CF于点D，且BD⊥BC，下列结论：①BC平分∠ABG；②AC//BG；③若∠A = α，则∠BDF = 180° - $\frac{α}{2}$；④与∠DBE互余的角有2个. 其中正确的为________（填序号）.
　　　　　

答案： 答案 ①②③
解析
∵BD⊥BC，
∴∠DBC=90°，
∴∠EBD+∠ABC=180° - 90° = 90°，∠DBG + ∠CBG = 90°，
∵BD平分∠EBG，
∴∠EBD = ∠DBG，
∴∠ABC = ∠GBC，即BC平分∠ABG，故①正确；
∵AE//CF，
∴∠ABC = ∠BCG，
∵CB平分∠ACG，
∴∠ACB = ∠BCG，
∵∠ABC = ∠GBC，
∴∠ACB = ∠GBC，
∴AC//BG，故②正确；
∵AC//BG，∠A = α，
∴∠EBG = ∠A = α，
∵∠EBD = ∠DBG，
∴∠EBD=$\frac{1}{2}$∠EBG=$\frac{\alpha}{2}$，
∵AB//CF，
∴∠EBD+∠BDF=180°，
∴∠BDF=180°-∠EBD=180°-$\frac{\alpha}{2}$，故③正确；
与∠DBE互余的角有∠ABC，∠CBG，∠ACB，∠BCG，共4个，故④错误.故正确的结论为①②③.

三、解答题（共40分）

答案：

19. （2023甘肃天水武山一模）（6分）如图，直线AB和CD相交于O点，OE⊥CD于O，∠EOF = 142°，∠BOD：∠BOF = 1：3，求∠AOF的度数.（M7207001）
　　　　　　　　　　　　

答案： 解析
∵OE⊥CD，
∴∠EOD=90°.
∵∠EOF=142°，
∴∠DOF=142°-90°=52°.
∵∠BOD : ∠BOF = 1 : 3，
∴∠BOD=$\frac{1}{2}$∠DOF = 26°.
∴∠BOF=∠BOD+∠DOF=78°.
∵∠AOF + ∠BOF = 180°，
∴∠AOF = 180° - ∠BOF = 102°.

20. （2024江苏南京鼓楼月考）（6分）证明：平行于同一条直线的两条直线平行.
请根据图形写出已知、求证及证明.
已知：
求证：
证明：
a__________
b__________
c__________

答案：
解析 答案不唯一，如：
已知：b//a，c//a.
求证：b//c.
证明：作直线l，l与直线a，b，c的交点依次为A，B，C，如图所示，

∵b//a(已知)，
∴∠1=∠2(两直线平行，同位角相等)，
又
∵c//a(已知)，
∴∠1=∠3(两直线平行，同位角相等)，
∴∠2=∠3(等式的基本事实)，
∴b//c(同位角相等，两直线平行).

21. （2024内蒙古巴彦淖尔月考）（7分）如图所示的是由边长为1的小正方形组成的网格，△ABC的顶点都在格点上，请分别按下列要求完成解答：（M7207008）
（1）平移△ABC，使顶点A平移到D处，顶点B平移后的对应点为E，画出平移后的△DEF.
（2）在（1）的条件下，连接AD，BE，则BE与AD的位置关系为________，DF与AC的数量关系为________.
（3）在（1）的条件下，求线段AB在平移过程中扫过的面积.
　　　　　　　　　　　　

答案：
解析
(1)如图，由题意得，△ABC向左平移2格，向上平移3格，得到的△DEF即为所求.

(2)如图，BE与AD的位置关系为平行，DF与AC的数量关系为相等.
(3)线段AB扫过的面积为5×4 - 2×$\frac{1}{2}$×3×1 - 2×$\frac{1}{2}$×3×2 = 20 - 3 - 6 = 11.