《2025年5年中考3年模拟七年级数学下册人教版》

15.[新独家原创]若x - 2024的立方根和算术平方根都等于它本身,则x =________.(M7208001)

答案： 15答案 2025或2024
解析 立方根等于本身的数是0，-1，1，算术平方根等于本身的数是0，1，
所以x - 2024 = 1或x - 2024 = 0，
解得x = 2025或x = 2024.

16.(2023山东滨州阳信期中改编)观察$:\sqrt{0.06137}≈0.2477,\sqrt{6.137}≈2.477,\sqrt[3]{6.137}≈1.8308,\sqrt[3]{6137}≈18.308.$推测:若$\sqrt[3]{x}≈0.18308,$则x≈________.

答案： 16答案 0.006137
解析
∵$\sqrt[3]{6.137}$≈1.8308，$\sqrt[3]{x}$≈0.18308，
∴x≈0.006137.

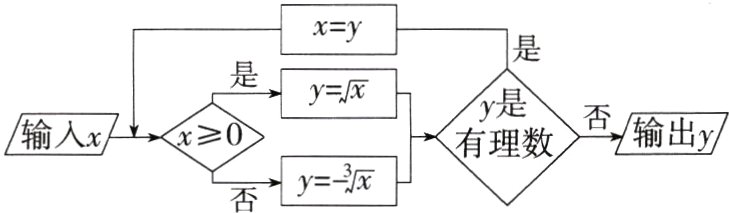
17.跨信息科技.计算程序如图所示的是小明用计算机设计的计算小程序,当输入的x的值为 - 64时,输出的y的值是________.
　

答案： 17答案 $\sqrt{2}$
解析 当输入的x的值为 - 64时，y = -$\sqrt[3]{-64}$ = 4，4是有理数；y = $\sqrt{4}$ = 2，2是有理数；y = $\sqrt{2}$，$\sqrt{2}$不是有理数，输出.
∴当输入的x的值为 - 64时，输出的y的值是$\sqrt{2}$.

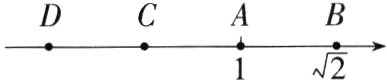
18.(2023河北邯郸期中)如图,数轴上从左到右依次有D,C,A,B四点,点A,B分别表示1和$\sqrt{2},$点C到点D的距离与点B到点A的距离相等,设点C表示的数为x.
(1)当D表示的数为0时,x的值是________.
(2)当D表示的数为$ - 2\sqrt{2}$时
①x的值是________;
②若m为x - 2的相反数,n为x + 2的绝对值,则m - n的值为________.
　　　　　

答案： 18答案
(1)$\sqrt{2}$ - 1
(2)① - $\sqrt{2}$ - 1；②4
解析
(1)由题意可得，x - 0 = $\sqrt{2}$ - 1，
∴x = $\sqrt{2}$ - 1.
(2)①由题意可得，x - (-2$\sqrt{2}$) = $\sqrt{2}$ - 1，解得x = - $\sqrt{2}$ - 1.
②
∵x = - $\sqrt{2}$ - 1，m为x - 2的相反数，n为x + 2的绝对值，
∴m = 2 - (-$\sqrt{2}$ - 1)=3 + $\sqrt{2}$，n = |(-$\sqrt{2}$ - 1)+2| = $\sqrt{2}$ - 1，
∴m - n = 3 + $\sqrt{2}$ - ($\sqrt{2}$ - 1)=4.

三、解答题(共40分)
19.(2024江西赣州于都期中)(6分)课堂上,老师让同学们从下列数中找一个无理数$:-\frac{22}{7},-\sqrt{2},\vert -\frac{1}{2}\vert,0,2\pi,-\sqrt[3]{8}.$甲找的数是$-\frac{22}{7},$乙找的数是$-\sqrt{2},$丙找的数是$2\pi.(M7208002)$
(1)甲、乙、丙三个人中,找错的是________.
(2)请将老师所给的数按要求填入相应的区域内.
正实数 负实数
... ...
　　

答案： 19解析
(1)甲.
(2)将$\left|-\frac{1}{2}\right|$，$2\pi$填入正实数的区域内.
将$-\frac{22}{7}$，$-\sqrt{2}$，$-\sqrt[3]{8}$填入负实数的区域内.

20.(2024重庆渝中期末)(6分)计算:(M7208003)
$(1)\sqrt{(-4)^2}-\sqrt[3]{-27}+\vert 1 - \sqrt{2}\vert.$
$(2)\sqrt{2\frac{1}{4}}+\sqrt{3}\times(\sqrt{3}-\frac{1}{\sqrt{3}}).$

答案： 20解析
(1)$\sqrt{(-4)^2}$ - $\sqrt[3]{-27}$ + |1 - $\sqrt{2}$|
= 4 - (-3) + $\sqrt{2}$ - 1 = 4 + 3 + $\sqrt{2}$ - 1 = 6 + $\sqrt{2}$.
(2)$\sqrt{2\frac{1}{4}}$ + $\sqrt{3}$×($\sqrt{3}$ - $\frac{1}{\sqrt{3}}$)
=$\frac{3}{2}$ + 3 - 1 = $\frac{7}{2}$.

21.(2023山东聊城期中)(6分)求下列各式中x的值.(M7208001)
(1)4x² - 3 = 6.
(2)2(x + 1)³ + 16 = 0.

答案： 21解析
(1)移项，得4x² = 6 + 3，
合并同类项，得4x² = 9，
系数化为1，得x² = $\frac{9}{4}$，
开平方，得x = ±$\sqrt{\frac{9}{4}}$，解得x = $\frac{3}{2}$或x = -$\frac{3}{2}$.
(2)
∵2(x + 1)³ + 16 = 0，
∴2(x + 1)³ = -16，
∴(x + 1)³ = -8，
∴x + 1 = $\sqrt[3]{-8}$ = -2，解得x = -3.