《2025年5年中考3年模拟七年级数学下册人教版》

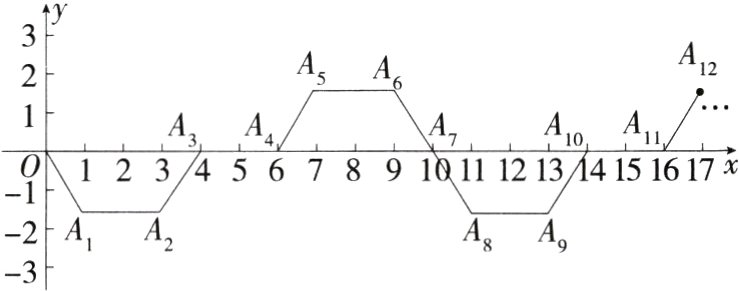
18.(2024黑龙江绥化中考,21,)如图，已知A₁(1,-√3)，A₂(3,-√3)，A₃(4,0)，A₄(6,0)，A₅(7,√3)，A₆(9,√3)，A₇(10,0)，A₈(11,-√3)，……，依此规律，点A₂₀₂₄的坐标为________.(M7209002)

答案： 答案$ (2891,-\sqrt{3})$解析 由题可知，点$A_1$的坐标为$(1,-\sqrt{3})，$点$A_2$的坐标为$(3,-\sqrt{3})，$点$A_3$的坐标为(4,0)，点$A_4$的坐标为(6,0)，点$A_5$的坐标为$(7,\sqrt{3})，$点$A_6$的坐标为$(9,\sqrt{3})，$点$A_7$的坐标为(10,0)，点$A_8$的坐标为$(11,-\sqrt{3})，$点$A_9$的坐标为$(13,-\sqrt{3})，$点$A_{10}$的坐标为(14,0)，点$A_{11}$的坐标为(16,0)，点$A_{12}$的坐标为$(17,\sqrt{3})，$点$A_{13}$的坐标为$(19,\sqrt{3})，$点$A_{14}$的坐标为(20,0)，……，由此可见，每七个点为一个循环，每增加一个循环，循环中对应位置的点的横坐标增加10，且纵坐标按$-\sqrt{3}，$$-\sqrt{3}，$0，0，$\sqrt{3}，$$\sqrt{3}，$0循环出现。因为2024÷7 = 289……1，所以$A_{2024}$的横坐标为1 + 289×10 = 2891，纵坐标为$-\sqrt{3}，$即点$A_{2024}$的坐标为$(2891,-\sqrt{3})。$

19.(2024北京海淀期中,16,)在平面直角坐标系xOy中，若将横、纵坐标之和为k的点记作“k和点”，则以下四个结论：①第二象限内有无数个“2和点”；②第一、三象限的角平分线上的“3和点”有两个；③y轴上没有“5和点”；④若第三象限内没有“k和点”，则k≥0.其中正确结论的序号是________.

答案： 答案 ①④
解析 ①第二象限内有无数个“2和点”，说法正确；②第一、三象限的角平分线上的“3和点”只有1个，即(1.5,1.5)，原说法错误；③y轴上有1个“5和点”，即(0,5)，原说法错误；④若第三象限内没有“k和点”，则k≥0，说法正确。故正确结论的序号是①④。

20.(2023江西新余期中改编,19,)已知点P(2m + 2,m - 3)，分别根据下列条件，求出点P的坐标.
(1)点P的纵坐标比横坐标大3.
(2)点P到x轴的距离为2，且在第四象限.

答案： 解析
(1)根据题意有m - 3 - (2m + 2) = 3，
∴m = -8，
∴2m + 2 = -14，m - 3 = -11，
∴P(-14,-11)。
(2)
∵|m - 3| = 2，
∴m = 1或m = 5，
∴点P的坐标为(4,-2)或(12,2)，
∵点P在第四象限，
∴点P的坐标为(4,-2)。

21.跨英语·单词 推理能力 两个小伙伴拿着如图所示的密码表玩听声音猜动物的游戏，若“咚咚 - 咚咚，咚 - 咚，咚咚咚 - 咚”表示的单词是DOG，也就是说，表示的动物是狗，则“咚咚 - 咚，咚咚咚 - 咚咚，咚 - 咚咚咚”表示的动物是（M7209002）（ ）

A.狐狸
B.猫
C.蜜蜂
D.牛

答案： B 由题意知，“咚咚 - 咚咚”对应D(2,2)，“咚 - 咚”对应O(1,1)，“咚咚咚 - 咚”对应G(3,1)。
∴“咚咚 - 咚”对应C(2,1)，“咚咚咚 - 咚咚”对应A(3,2)，“咚 - 咚咚咚”对应T(1,3)。故表示的单词是CAT，也就是说，表示的动物是猫。故选B。

22.运算能力 (2023北京通州期中)在平面直角坐标系xOy中，已知点M的坐标为(2 - t,2t)，将点M到x轴的距离记为d₁，到y轴的距离记为d₂.
(1)若t = 3，则d₁ + d₂ = ________.
(2)若t＜0，d₁ = d₂，求点M的坐标.
(3)若点M在第二象限，且md₁ - 5d₂ = 10(m为常数)，求m的值.

答案： 解析
∵点M的坐标为(2 - t,2t)，将点M到x轴的距离记为$d_1，$到y轴的距离记为$d_2，$
∴$d_1 = |2t|，$$d_2 = |2 - t|。$
(1)
∵t = 3，
∴$d_1 = |2t| = |2×3| = 6，$$d_2 = |2 - t| = |2 - 3| = 1，$
∴$d_1 + d_2 = 6 + 1 = 7。$故答案为7。
(2)
∵t ＜ 0，
∴2 - t ＞ 0，2t ＜ 0，
∴d_1 = |2t| = -2t，d_2 = |2 - t| = 2 - t，
∵d_1 = d_2，
∴-2t = 2 - t，
∴t = -2，
∴2 - t = 2 - (-2) = 4，2t = 2×(-2) = -4，
∴M(4,-4)。
(3)
∵点M在第二象限，
∴2 - t ＜ 0，2t ＞ 0，
∴$d_1 = |2t| = 2t，$$d_2 = |2 - t| = t - 2，$
∵$md_1 - 5d_2 = 10，$
∴m×2t - 5×(t - 2) = 10，整理得(2m - 5)t = 0，
∵t≠0，
∴2m - 5 = 0，
∴$m = \frac{5}{2}。$

例(2024天津滨海新区期末)已知点B是x轴负半轴上一点,且与点A(2,0)的距离为4,则点B 的坐标为________.(M7209002)

答案： 答案 (-2,0)
解析 在x轴上，与A(2,0)的距离是4的点为(2 - 4,0)和(2 + 4,0)，
∵B与点A(2,0)的距离为4，B是x轴负半轴上一点，
∴B(-2,0)。

1.若点P(a+1,2a−6)在y轴上,则点P的坐标为________.(M7209002)

答案： 答案 (0,-8)
解析
∵点P(a + 1,2a - 6)在y轴上，
∴a + 1 = 0，解得a = -1，
∴2a - 6 = -8，
∴P的坐标为(0,-8)。

2.已知点A(x−5,2x−4)在第一、三象限的角平分线上,则点A的坐标是________.

答案： 答案 (-6,-6)
解析
∵点A(x - 5,2x - 4)在第一、三象限的角平分线上，
∴x - 5 = 2x - 4，解得x = -1，
∴x - 5 = -1 - 5 = -6，2x - 4 = -2 - 4 = -6，
∴A(-6,-6)。

3.已知点P,Q的坐标分别为(2m−5,m−1),(n +2,2n−1),若点P在第二、四象限的角平分线上,点Q在第一、三象限的角平分线上,则$m^{n+1}$的值为________.

答案： 答案 16
解析
∵点P(2m - 5,m - 1)在第二、四象限的角平分线上，
∴2m - 5 + m - 1 = 0，解得m = 2。
∵点Q(n + 2,2n - 1)在第一、三象限的角平分线上，
∴n + 2 = 2n - 1，解得n = 3。
∴$m^{n + 1}=2^{3 + 1}=2^{4}=16。$