《2025年5年中考3年模拟七年级数学下册人教版》

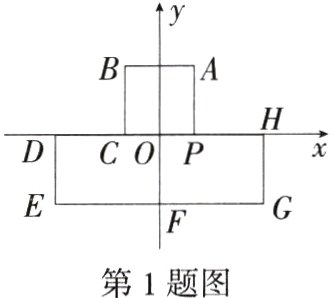
1.(2024北京西城期中)如图，在平面直角坐标系中，AB，EG均与x轴平行，BC，DE，HG，AP均与y轴平行，点D、C、P、H在x轴上，A(1,2)，B(-1,2)，D(-3,0)，E(-3,-2)，G(3,-2)，把一条长为2039个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处，并按A→B→C→D→E→F→G→H→P→A...的规律紧绕在图形“凸”的边上，则细线另一端所在位置的点的坐标是(M7209004) (　　　)
　　
A.(1,1)　　　　　　
　B.(1,2)
C.(-1,2)　　　　　
　D.(-1,-2)

答案： 1A易知图形“凸”的周长为20个单位长度，
∵2039÷20=101……19,
∴细线另一端所在位置的点在P正上方1个单位长度处，坐标为(1,1).
　故选A.

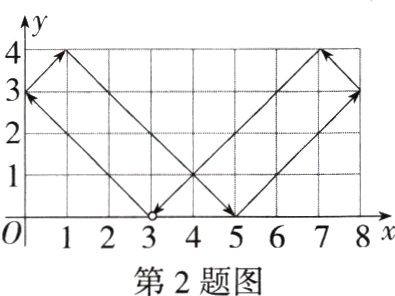
2.(2022山东济宁曲阜期中改编)如图，小球开始时位于(3,0)处，沿如图所示的方向击球，小球碰到球桌边会改变轨迹，其运动轨迹如图所示。如果小球开始时位于(1,0)处，仍按原来的方向击球，小球第一次碰到球桌边时，小球的位置是(0,1)，当小球第2026次碰到球桌边时，小球的位置是________。
　　

答案：
答案　(8,1)
　解析　如图，小球开始时位于(1,0)处，
　　　　　　
　第1次碰到球桌边时，小球的位置是(0,1)，
　第2次碰到球桌边时，小球的位置是(3,4)，
　第3次碰到球桌边时，小球的位置是(7,0)，
　第4次碰到球桌边时，小球的位置是(8,1)，
　第5次碰到球桌边时，小球的位置是(5,4)，
　第6次碰到球桌边时，小球的位置是(1,0)，
　第7次碰到球桌边时，小球的位置是(0,1)，
　易知6次为一个循环，因为2026÷6=337……4,所以当小球第2026次碰到球桌边时，小球的位置是(8,1).

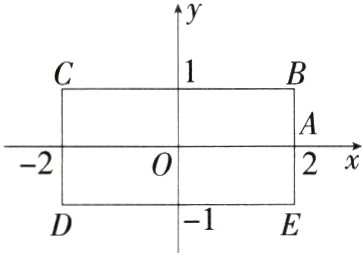
3.(2024湖北武汉期末)如图，长方形BCDE中，BC和DE均平行于x轴，CD和BE均平行于y轴，物体甲和物体乙由点A(2,0)同时出发，沿长方形BCDE的边做环绕运动，物体甲按逆时针方向以每秒1个单位长度的速度匀速运动，物体乙按顺时针方向以每秒2个单位长度的速度匀速运动，则两个物体运动后的第2024个相遇地点的坐标是________。(M7209004)
　　　　　

答案： 答案　(-1,-1)
　解析　由题图可知，长方形BCDE的周长为12个单位长度，
∴甲、乙两个物体每次相遇的时间间隔为$\frac{12}{1 + 2}$ = 4秒,
∴甲、乙两个物体的相遇地点的坐标依次为(-1,1),(-1,-1),(2,0),(-1,1),……
∴相遇地点每3个为一个循环，
∵2024 = 3×674 + 2,
∴第2024个相遇地点的坐标是(-1,-1).

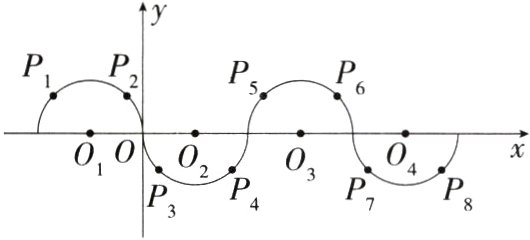
4.(2024湖北武汉江岸期末)如图，在平面直角坐标系中，半径均为2个单位长度的半圆O₁,O₂,O₃,…,组成一条平滑的曲线，其中O₁(-2,0)，O₂(2,0)，O₃(6,0)，……，在每一段半圆上均有靠近直径端点的两个四等分点，P₁(-2 - √2,√2)，P₂(-2 + √2,√2)，P₃(2 - √2,-√2)，P₄(2 + √2,-√2)，P₅(6 - √2,√2)，P₆(6 + √2,√2)，……，则点P₂₀₂₄的坐标为(M7209004) (　　　)
　　　
A.(4 046 + √2,-√2)　
　B.(4 046 - √2,√2)
C.(4 042 + √2,-√2)　
　D.(4 042 - √2,√2)

答案： 4C
∵$O_1(-2,0)$，$O_2(2,0)$，$O_3(6,0)$，$O_4(10,0)$，……，
∴$O_n(4n - 6,0)(n≥1)$，由题意可知，$P_{2024}$为半圆$O_{1012}$上靠近直径右端点的四等分点，$O_{1012}(4042,0)$，观察题图可知，半圆$O_1$上靠近直径右端点的四等分点为$P_2(-2+\sqrt{2},\sqrt{2})$，半圆$O_2$上靠近直径右端点的四等分点为$P_4(2+\sqrt{2},-\sqrt{2})$，半圆$O_3$上靠近直径右端点的四等分点为$P_6(6+\sqrt{2},\sqrt{2})$，半圆$O_4$上靠近直径右端点的四等分点为$P_8(10+\sqrt{2},-\sqrt{2})$，……，以此类推，$P_{2024}$为半圆$O_{1012}$上靠近直径右端点的四等分点，
∴$P_{2024}(4042+\sqrt{2},-\sqrt{2})$，故选C.