第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
1. 如图,已知$\triangle ABC\cong \triangle DEF$,$BE=3$,$AE=1$,则$DE$的长是(
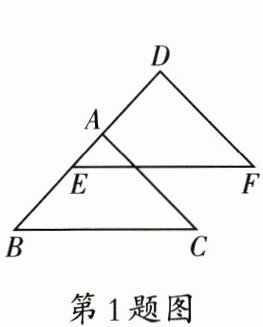
A.5
B.4
C.3
D.2
B
)
A.5
B.4
C.3
D.2
答案:
1.B
2. 如图,已知$\triangle ABC\cong \triangle FED$,则下列结论错误的是(
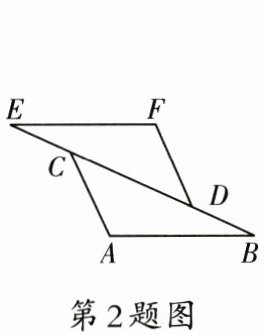
A.$EC=BD$
B.$EF// AB$
C.$\angle E=\angle FDE$
D.$S_{\triangle ABC}=S_{\triangle FED}$
C
)
A.$EC=BD$
B.$EF// AB$
C.$\angle E=\angle FDE$
D.$S_{\triangle ABC}=S_{\triangle FED}$
答案:
2.C
3. 如图,李明站在河边的点$A$处,在河对面(正北方向)的点$B$处有一电线塔,他想知道此时电线塔离他有多远,于是他向正西方向走了10米到达一棵树$C$处,接着再向西走了10米到达$D$处,然后他左转$90^{\circ}$直行,当他看到电线塔、树与自己现处的位置$E$在一条直线时,测得$DE=20$米,则电线塔离点$A$的距离是(
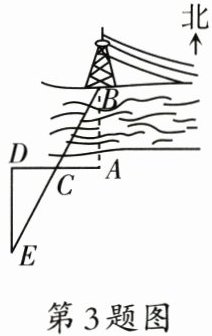
A.10米
B.20米
C.30米
D.40米
B
)
A.10米
B.20米
C.30米
D.40米
答案:
3.B
4. 如图,在$\triangle ABC$和$\triangle DEF$中,点$B,F,C,E$在同一直线上,$\angle ACB=\angle DFE$,$BF=EC$.只添加一个条件,不能判定$\triangle ABC\cong \triangle DEF$的是(

A.$AC=DF$
B.$AB=DE$
C.$\angle A=\angle D$
D.$\angle B=\angle E$
B
)
A.$AC=DF$
B.$AB=DE$
C.$\angle A=\angle D$
D.$\angle B=\angle E$
答案:
4.B
5. 如图,在$\triangle ABC$中,$F$是高$AD,BE$的交点,$AD=BD$,$BC=6$,$CD=2$,则线段$AF$的长度为(
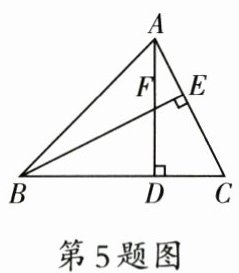
A.2
B.1
C.4
D.3
A
)
A.2
B.1
C.4
D.3
答案:
5.A
6. 如图,在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$AC=8$,$BC=4$,$PQ=AB$,点$P$与点$Q$分别在$AC$和$AC$的垂线$AD$上移动,则当$AP=$(
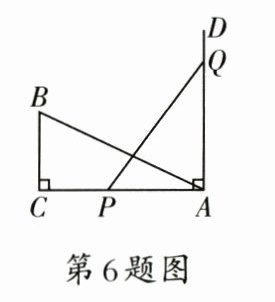
A.4
B.8
C.4或8
D.不能确定
C
)时,$\triangle ABC\cong \triangle APQ$.
A.4
B.8
C.4或8
D.不能确定
答案:
6.C
7. 如图,$\triangle ABC\cong \triangle DEF$,若$BF=8$,$BE=2$,则$EC$的长为
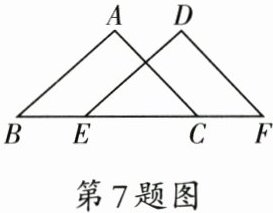
4
.
答案:
7.4
8. 李明不慎将一块三角形玻璃摔碎成如图所示的4块,他选择带第4块去玻璃店,就能配一块与原来一样大小的三角形玻璃.他选择第4块的理论依据是
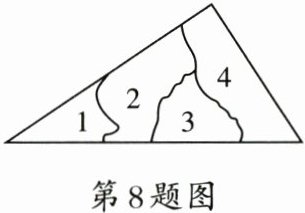
ASA
.(三角形全等的判定定理的简称)
答案:
8.ASA
9. 如图,在$\triangle ABC$与$\triangle DEF$中,$AB=DE$,$BC=EF$,且点$A$在$EF$上,点$D$在$BC$上,请添加一个条件:
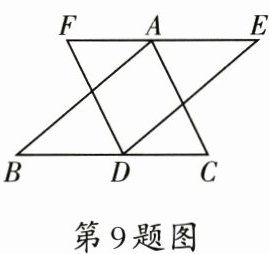
∠B=∠E(或AC=DF,答案不唯一)
,能判定$\triangle ABC\cong \triangle DEF$.
答案:
9.∠B=∠E(或AC=DF,答案不唯一)
查看更多完整答案,请扫码查看


