《2025年优学1+1评价与测试八年级数学上册人教版》

1. 计算$\frac{8x}{x - y} · \frac{x - y}{8y}$的结果是(C)

A.$\frac{y}{x}$
B.$- \frac{x}{y}$
C.$\frac{x}{y}$
D.$- \frac{y}{x}$

答案： 1.C

2. 下列分式计算正确的是(B)

A.$\frac{a}{b} · \frac{c}{d} = \frac{ad}{bc}$
B.$\frac{m^{4}}{n^{5}} · \frac{n^{4}}{m^{3}} = \frac{m}{n}$
C.$(\frac{2a}{a - b})^{2} = \frac{4a^{2}}{a^{2} - b^{2}}$
D.$(\frac{3x}{4y})^{3} = \frac{3x^{3}}{4y^{3}}$

答案： 2.B

3. 计算$\frac{y}{x} ÷ \frac{y}{2} · \frac{2}{y}$的结果是(A)

A.$\frac{4}{xy}$
B.$\frac{1}{2}x$
C.$\frac{y}{x}$
D.$2y$

答案： 3.A

4. 若$x = 2025$，则式子$\frac{x^{2} - 2x + 1}{x^{2} - 1} ÷ \frac{x - 1}{x^{2} + x}$的值为(C)

A.2023
B.2024
C.2025
D.1

答案： 4.C

5. 计算$(\frac{2x}{y^{2}})^{3} · (\frac{2y}{x})^{2} ÷ (- \frac{2y}{x})$的结果是(C)

A.$- \frac{8x^{3}}{y^{6}}$
B.$\frac{8x^{3}}{y^{6}}$
C.$- \frac{16x^{2}}{y^{5}}$
D.$\frac{16x^{2}}{y^{5}}$

答案： 5.C

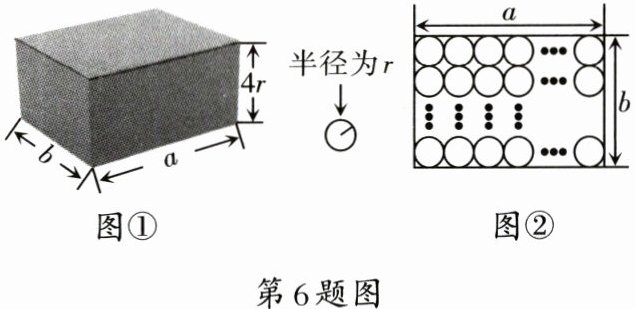
6. 如图①，某品牌饮料的包装箱是一个长、宽、高分别为$a$，$b$，$4r$的长方体纸箱，饮料瓶可近似看成底面半径为$r$，高为$4r$的圆柱体。如图②，若纸箱里装满了一层饮料，那么纸箱的空间利用率(听装饮料总体积与纸箱体积的比)为(A)

A.$\frac{\pi}{4}$
B.$\pi r^{2}$
C.$\frac{\pi r^{2}}{ab}$
D.$\frac{\pi r^{2}}{4ab}$

答案： 6.A 解析：
∵长方体纸盒装满了一层底面半径为$r$，高为$4r$的圆柱体的听装饮料，
∴长方体的长边放置的圆柱体的数量为$\frac{a}{2r}$，
长方体的宽边放置的圆柱体的数量为$\frac{b}{2r}$，
∴听装饮料的数量为$\frac{a}{2r} · \frac{b}{2r} = \frac{ab}{4r^{2}}$
∴听装饮料的总体积:$\pi r^{2} · 4r · \frac{ab}{4r^{2}} = abr\pi$，
纸箱容积为$a · b · 4r = 4abr$，
∴纸盒的空间利用率为$\frac{abr\pi}{4abr} = \frac{\pi}{4}$。

7. 计算：$(\frac{- 2a^{2}}{3x^{2}y})^{2} =$ _ 。

答案： 7.$\frac{4a^{4}}{9x^{4}y^{2}}$

8. 如果代数式$m^{2} + 2m = 1$，那么$\frac{m^{2} + 4m + 4}{m} ÷ \frac{m + 2}{m^{2}}$的值为1_ 。

答案： 8.1

9. 李明在进行两个多项式的乘法运算时，不小心把乘$\frac{x + y}{2}$错抄成乘$\frac{x}{2}$，结果得到$3x^{2} - xy$，则正确的计算结果是$3x^{2} + 2xy - y^{2}$_ 。

答案： 9.$3x^{2} + 2xy - y^{2}$

10. 如果$\frac{m}{3} = \frac{n}{2} \neq 0$，那么代数式$\frac{3m - n}{4m^{2} - n^{2}}$$\frac{7}{4}$$· (2m + n)$的值是 _ 。

答案： 10.$\frac{7}{4}$

11. （10分）计算：
(1)$\frac{2a}{3b} · \frac{- 9b^{2}}{4a^{3}}$；
(2)$(\frac{x^{2}}{y})^{3} ÷ (- \frac{x}{y^{2}})^{2}$；
(3)$(xy - x^{2}) ÷ \frac{x^{2} - 2xy + y^{2}}{xy} · \frac{x - y}{x^{2}}$。

答案： 11.解:
(1)$\frac{-3b}{2a^{2}}$
(2)$x^{4}y$
(3)$-y$