第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
21. (6分)对于任意的正整数$n$,代数式$n(n + 7)-(n + 3)(n - 2)$的值总能被6整除,试说明理由.
答案:
21.解:
∵n(n+7)-(n+3)(n-2)
=n²+7n-(n²-2n+3n-6)
=n²+7n-n²+2n-3n+6
=6n+6
=6(n+1)
∴对于任意的正整数n,代数式
n(n+7)-(n+3)(n-2)的值总能被6整除.
∵n(n+7)-(n+3)(n-2)
=n²+7n-(n²-2n+3n-6)
=n²+7n-n²+2n-3n+6
=6n+6
=6(n+1)
∴对于任意的正整数n,代数式
n(n+7)-(n+3)(n-2)的值总能被6整除.
22. (10分)阅读下列材料:利用完全平方公式,将多项式$x^{2}+bx + c$变形为$(x + m)^{2}+n$的形式,然后由$(x + m)^{2}\geqslant0$就可求出多项式$x^{2}+bx + c$的最小值.
例:求多项式$x^{2}-4x + 5$的最小值.
解:$x^{2}-4x + 5 = x^{2}-4x + 4 + 1=(x - 2)^{2}+1$.因为$(x - 2)^{2}\geqslant0$,所以$(x - 2)^{2}+1\geqslant1$当$x = 2$时,$(x - 2)^{2}+1 = 1$,因此$(x - 2)^{2}+1$有最小值,最小值为1,即$x^{2}-4x + 5$的最小值为1.
通过阅读,理解材料的解题思路,请解决以下问题:
(1)【理解探究】已知代数式$A = x^{2}+8x + 7$.求$A$的最小值;
(2)【类比应用】张大爷家有甲、乙两块长方形菜地,已知甲菜地的两边长分别是$(5a + 1)$米,$(2a + 2)$米,乙菜地的两边长分别是$(3a + 8)$米,$(3a - 2)$米.试比较这两块菜地的面积$S_{甲}$和$S_{乙}$的大小,并说明理由;
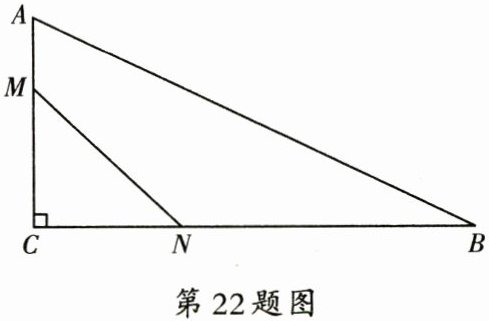
(3)【拓展升华】如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 8\ cm$,$BC = 16\ cm$,点$M$,$N$分别是线段$AC$和$BC$上的动点,点$M$从点$A$出发以$1\ cm/s$的速度向点$C$运动.同时,点$N$从点$C$出发以$2\ cm/s$的速度向点$B$运动,当其中一点到达终点时,两点同时停止运动.设运动的时间为$t$(单位:$s$),则当$t$的值为多少时,$\triangle MCN$的面积最大?最大值为多少?
例:求多项式$x^{2}-4x + 5$的最小值.
解:$x^{2}-4x + 5 = x^{2}-4x + 4 + 1=(x - 2)^{2}+1$.因为$(x - 2)^{2}\geqslant0$,所以$(x - 2)^{2}+1\geqslant1$当$x = 2$时,$(x - 2)^{2}+1 = 1$,因此$(x - 2)^{2}+1$有最小值,最小值为1,即$x^{2}-4x + 5$的最小值为1.
通过阅读,理解材料的解题思路,请解决以下问题:
(1)【理解探究】已知代数式$A = x^{2}+8x + 7$.求$A$的最小值;
(2)【类比应用】张大爷家有甲、乙两块长方形菜地,已知甲菜地的两边长分别是$(5a + 1)$米,$(2a + 2)$米,乙菜地的两边长分别是$(3a + 8)$米,$(3a - 2)$米.试比较这两块菜地的面积$S_{甲}$和$S_{乙}$的大小,并说明理由;
(3)【拓展升华】如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 8\ cm$,$BC = 16\ cm$,点$M$,$N$分别是线段$AC$和$BC$上的动点,点$M$从点$A$出发以$1\ cm/s$的速度向点$C$运动.同时,点$N$从点$C$出发以$2\ cm/s$的速度向点$B$运动,当其中一点到达终点时,两点同时停止运动.设运动的时间为$t$(单位:$s$),则当$t$的值为多少时,$\triangle MCN$的面积最大?最大值为多少?

答案:
22.解:
(1)A=x²+8x+7=(x+4)²-9
∴A的最小值为-9;
(2)S甲-S乙=(5a+1)(2a+2)-(3a+8)(3a-2)
=10a²+10a+2a+2-(9a²-6a+24a-16)
=a²-6a+18
=(a-3)²+9
∴S甲-S乙的最小值为9,恒大于零,
综上所述:S甲>S乙;
(3)由题意知:AM=t,CN=2t
∵∠C=90°,
∴S△MCN=$\frac{1}{2} × 2t × (8-t)=t · (8-t)=8t-t^{2}$
=-(t-4)²+16
当t=4时,S有最大值,即Smax=16.
(1)A=x²+8x+7=(x+4)²-9
∴A的最小值为-9;
(2)S甲-S乙=(5a+1)(2a+2)-(3a+8)(3a-2)
=10a²+10a+2a+2-(9a²-6a+24a-16)
=a²-6a+18
=(a-3)²+9
∴S甲-S乙的最小值为9,恒大于零,
综上所述:S甲>S乙;
(3)由题意知:AM=t,CN=2t
∵∠C=90°,
∴S△MCN=$\frac{1}{2} × 2t × (8-t)=t · (8-t)=8t-t^{2}$
=-(t-4)²+16
当t=4时,S有最大值,即Smax=16.
查看更多完整答案,请扫码查看


