第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
1. 点$A(3,5)$关于$x$轴的对称点的坐标为(
A.$(3,-5)$
B.$(-3,-5)$
C.$(-3,5)$
D.$(-5,3)$
A
)A.$(3,-5)$
B.$(-3,-5)$
C.$(-3,5)$
D.$(-5,3)$
答案:
1.A
2. 如图,给出了一个轴对称图形的一半,其中虚线是这个图形的对称轴,请你猜想整个图形是(
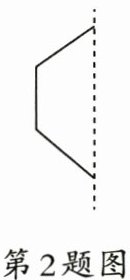
A.三角形
B.长方形
C.五边形
D.六边形
D
)
A.三角形
B.长方形
C.五边形
D.六边形
答案:
2.D
3. 将第一象限的“小旗”各点的横坐标分别乘$-1$,纵坐标保持不变,符合上述要求的图形是(

A.
B.
C.
D.
C
)
A.
B.
C.
D.
答案:
3.C
4. 室内墙壁上挂一平面镜,李明在平面镜内看到他背后墙上时钟的示数如图所示,则这时的实际时间应是(

A.$3:20$
B.$3:40$
C.$4:40$
D.$8:20$
B
)
A.$3:20$
B.$3:40$
C.$4:40$
D.$8:20$
答案:
4.B
5. 若$A$,$B$两点关于$x$轴对称,则下列说法正确的是(
A.线段$AB// x$轴
B.线段$AB\perp y$轴
C.线段$AB$垂直平分$x$轴
D.$x$轴垂直平分线段$AB$
D
)A.线段$AB// x$轴
B.线段$AB\perp y$轴
C.线段$AB$垂直平分$x$轴
D.$x$轴垂直平分线段$AB$
答案:
5.D
6. 如图,分别以$\triangle ABC$的边$AB$,$AC$所在直线为对称轴作$\triangle ABC$的对称图形$\triangle ABD$和$\triangle ACE$。$\angle BAC = 150^{\circ}$,线段$BD$与$CE$相交于点$O$,连接$BE$,$ED$,$DC$,$OA$。有如下结论:①$\angle EAD = 90^{\circ}$;②$\angle BOE = 60^{\circ}$;③$OA$平分$\angle BOC$;④$EA=\frac{1}{2}ED$;⑤$BP = EQ$。其中,正确的结论个数是(
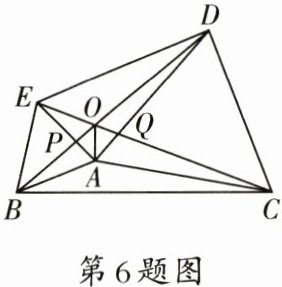
A.4个
B.3个
C.2个
D.1个
B
)
A.4个
B.3个
C.2个
D.1个
答案:
6.B 解析:
∵△ABD和△ACE是△ABC的轴对称图形,
∴∠BAD=∠CAE=∠BAC,AB=AE,AC=AD,
∴∠EAD=3∠BAC−360°=3×150°−360°=90°,
故①正确;
∴∠BAE=∠CAD=$\frac{1}{2}$(360°−90°−150°)=60°,
由翻折的性质得,∠AEC=∠ABD=∠ABC,
又
∵∠EPO=∠BPA,
∴∠BOE=∠BAE=60°,故②正确;
∵△ACE≌△ADB,
∴S_{△ACE}=S_{△ADB},BD=CE,
∴BD边上的高与CE边上的高相等,即点A到∠BOC两边的距离相等,
∴OA平分∠BOC,故③正确;
只有当AC=$\sqrt{3}$AB时,∠ADE=30°,
才有EA=$\frac{1}{2}$ED,故④错误;
在△ABP和△AEQ中,∠ABD=∠AEC,AB=AE,
∠BAE=60°,∠EAQ=90°,
∴BP<EQ,故⑤错误;
综上所述,结论正确的是①②③,共3个.
∵△ABD和△ACE是△ABC的轴对称图形,
∴∠BAD=∠CAE=∠BAC,AB=AE,AC=AD,
∴∠EAD=3∠BAC−360°=3×150°−360°=90°,
故①正确;
∴∠BAE=∠CAD=$\frac{1}{2}$(360°−90°−150°)=60°,
由翻折的性质得,∠AEC=∠ABD=∠ABC,
又
∵∠EPO=∠BPA,
∴∠BOE=∠BAE=60°,故②正确;
∵△ACE≌△ADB,
∴S_{△ACE}=S_{△ADB},BD=CE,
∴BD边上的高与CE边上的高相等,即点A到∠BOC两边的距离相等,
∴OA平分∠BOC,故③正确;
只有当AC=$\sqrt{3}$AB时,∠ADE=30°,
才有EA=$\frac{1}{2}$ED,故④错误;
在△ABP和△AEQ中,∠ABD=∠AEC,AB=AE,
∠BAE=60°,∠EAQ=90°,
∴BP<EQ,故⑤错误;
综上所述,结论正确的是①②③,共3个.
7. 如图,如果$AA'$,$BB'$都被$MN$垂直平分,那么$AB$和$A'B'$关于直线$MN$

对称
_ 。
答案:
7.对称
8. 剪纸艺术是我国最古老的民间艺术之一,很多剪纸作品体现了数学中的对称美。如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,点$E$的坐标为$(-2,-n)$,其关于$y$轴对称的点$F$的坐标$(2,1 - m)$,则$(n - m)^{2025}=$

−1
_ 。
答案:
8.−1
9. 在平面直角坐标系中,若点$A(a + 2,4 - b)$,$B(2b + 3,2a)$是关于$x$轴的对称点,则线段$AB$的长为
12
_ 。
答案:
9.12
10. 如图,在平面直角坐标系中,对$\triangle ABC$进行循环往复地轴对称变换。若原来点$A$的坐标是$(a,b)$,则经过第$2025$次变换后所得的$A$点坐标是

(a,−b)
_ 。
答案:
10.(a,−b)
解析:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2025÷4=506……1,
∴经过第2025次变换后所得的A点与第一次变换的位置相同,在第四象限,坐标为(a,−b).
解析:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2025÷4=506……1,
∴经过第2025次变换后所得的A点与第一次变换的位置相同,在第四象限,坐标为(a,−b).
查看更多完整答案,请扫码查看


