《2025年一本同步训练九年级数学上册人教版重庆专版》

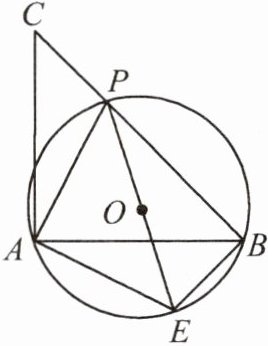
9. 如图,已知$\triangle ABC$是等腰直角三角形,P是斜边BC上一点(不与点B,C重合),PE是$\triangle ABP$的外接圆$\odot O$的直径.
(1)求证:$\triangle APE$是等腰直角三角形;
(2)若$\odot O$的直径为2,求$PB^{2}+PC^{2}$的值.

答案： 1. （1）证明：
因为$\triangle ABC$是等腰直角三角形，$\angle CAB = 90^{\circ}$，$\angle ABC=\angle ACB = 45^{\circ}$。
同弧所对的圆周角相等，$\angle AEP=\angle ABP$（$\overset{\frown}{AP}$所对的圆周角），$\angle ABP = 45^{\circ}$，所以$\angle AEP = 45^{\circ}$。
因为$PE$是$\odot O$的直径，所以$\angle PAE = 90^{\circ}$（直径所对的圆周角是直角）。
在$\triangle PAE$中，$\angle PAE = 90^{\circ}$，$\angle AEP = 45^{\circ}$，则$\angle APE=\angle AEP = 45^{\circ}$。
所以$AE = AP$，所以$\triangle APE$是等腰直角三角形。
2. （2）解：
连接$BE$。
因为$\angle PAE=\angle BAC = 90^{\circ}$，所以$\angle PAE-\angle PAB=\angle BAC-\angle PAB$，即$\angle BAE=\angle CAP$。
又因为$AE = AP$，$AB = AC$，根据$SAS$（边角边）可得$\triangle ABE\cong\triangle ACP$。
所以$\angle ABE=\angle ACP = 45^{\circ}$，$BE = CP$。
则$\angle PBE=\angle ABC+\angle ABE=45^{\circ}+45^{\circ}=90^{\circ}$。
在$Rt\triangle PBE$中，根据勾股定理$PB^{2}+BE^{2}=PE^{2}$。
因为$PE = 2$（$\odot O$的直径），$BE = CP$，所以$PB^{2}+PC^{2}=PE^{2}$。
所以$PB^{2}+PC^{2}=4$。
综上，（1）得证；（2）$PB^{2}+PC^{2}$的值为$4$。

10. 如图,$\odot O$是锐角三角形ABC的外接圆,$OD⊥AB,OE⊥BC,OF⊥AC$,垂足分别为D,E,F,连接DE,EF,FD.若$DE+DF=6.5,\triangle ABC$的周长为21,则EF的长为 (B)
A. 8
B. 4
C. 3.5
D. 3

答案： B

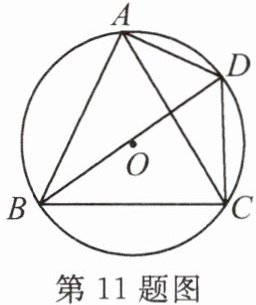
11. 如图,$\odot O$是等边三角形ABC的外接圆,D是$\widehat {AC}$上的一个动点(不与点A,C重合),有下列结论:①$∠ADB=∠BDC$;②$DA=DC$;③当DB最长时,$DB=2DC$;④$DA+DC=DB$.其中一定正确的结论有____.(填序号)


①③④

答案： ①③④

12. 如图,$\odot O$是$\triangle ABC$的外接圆,弦BD交AC于点E,$AE=DE,BC=CE$,过点O作$OF⊥AC$于点F,延长FO交BE于点G.若$DE=3,EG=2$,则$∠ACB$的度数为____,AB的长为____.

答案： $60^{\circ}$ 7

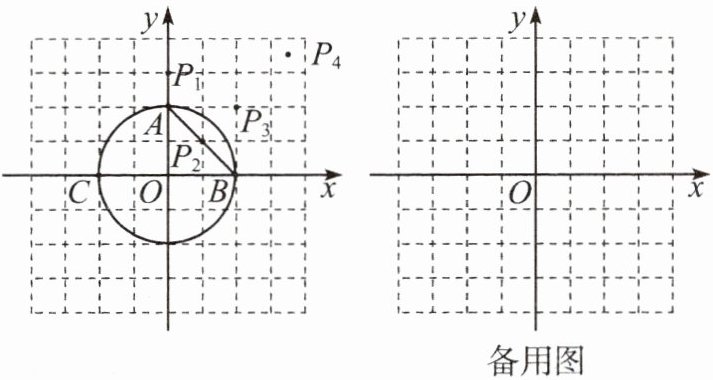
13. 在平面直角坐标系xOy中,$\odot O$的半径为1,MN为$\odot O$的弦.对于平面内的一点P,若点P关于MN的对称点恰好在$\odot O$内,则称点P为弦MN的“内称点”.已知点$A(0,1),B(1,0),C(-1,0).$
(1)如图,下列各点中,是弦AB的“内称点”的是____.(填序号)
①$P_{1}(0,\frac {3}{2})$;②$P_{2}(\frac {1}{2},\frac {1}{2})$;③$P_{3}(1,1)$;④$P_{4}(1+\frac {\sqrt {2}}{2},1+\frac {\sqrt {2}}{2})$.
①②③
(2)已知点D,E在$\odot O$上运动,且$DE=a$,若$\odot O$内的每一个点都能成为某一时刻弦DE的“内称点”,求a的取值范围.
$\sqrt{3}＜a\leqslant2$

答案：
(1)①②③
(2)$\sqrt{3}＜a\leqslant2$