《2025年一本同步训练九年级数学上册人教版重庆专版》

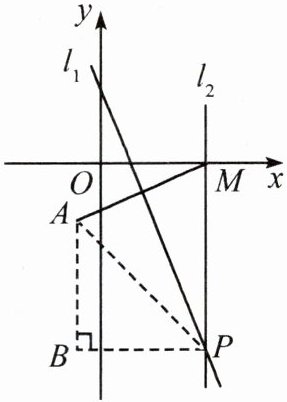
活动2 [提出问题]如图,在平面直角坐标系中,点A的坐标是(-1,-2),在x轴上任取一点M,完成以下操作步骤:
①连接AM,作线段AM的垂直平分线l₁,过点M作x轴的垂线l₂,记l₁,l₂的交点为P;
②在x轴上多次改变点M的位置,用①的方法得到相应的点P,把这些点用平滑的曲线连接起来,观察画出的曲线L,猜想它是我们学过的哪种曲线.

[观察实验]某数学兴趣小组在探究时发现在x轴上取几个特殊位置的点M,可以求出相对应的点P的坐标.
例如,取点M(-1,0),则点P的坐标为(-1,-1).
如图,取点M(4,0),过点P作直线x=-1的垂线,垂足为B,∴P(4,y),∴PM=-y.
在Rt△PAB中,根据勾股定理,得PA²=PB²+AB²=25+(-2-y)²(用含y的代数式表示).
∵点P在AM的垂直平分线上,∴PA=PM,∴PM²=PA²,
由此可列关于y的方程(-y)²=25+(-2-y)²,解得y=-29/4,∴P(4,-29/4).
[解决问题](1)完成以上填空;
(2)在x轴上多次改变点M的位置,按上述方法得到相应点P的坐标,并完成下列表格;
|点M的坐标|…|(-4,0)|(-3,0)|(-1,0)|(1,0)|(3,0)|(4,0)|…|
|----|----|----|----|----|----|----|----|----|
|点P的坐标|…|(-4,-13/4)|(-3,-2)|(-1,-1)|(1,-2)|(3,-5)|(4,-29/4)|…|
(3)该数学兴趣小组求出点P(x,y)所在曲线L的解析式为y=-1/4x²-1/2x-5/4;
(4)兴趣小组在建立平面直角坐标系时受纸张大小的限制,使点M只能在-7＜x＜6的范围内移动,则y的取值范围是y≤-1;
[拓展提升](5)若点A(m,d)(d＜0),猜想曲线L的最高点的坐标为(m,-d/2),说明理由.

答案： 1. （1）
当$M(-1,0)$时：
因为$l_{2}$是过$M(-1,0)$作$x$轴的垂线，所以$x = - 1$。
又因为$l_{1}$是$AM$的垂直平分线，$A(-1,-2)$，$M(-1,0)$，$AM$垂直于$x$轴，所以$AM$的垂直平分线$l_{1}$平行于$x$轴，$AM$中点纵坐标为$\frac{-2 + 0}{2}=-1$，所以$P(-1,-1)$。
2. （2）
当$M(-4,0)$时：
设$P(-4,y)$，$A(-1,-2)$，$PM=-y$，$PB = 3$，$AB=-2 - y$。
根据勾股定理$PA^{2}=PB^{2}+AB^{2}=9+(-2 - y)^{2}$，因为$PA = PM$，所以$(-y)^{2}=9+(-2 - y)^{2}$。
展开得$y^{2}=9 + 4 + 4y+y^{2}$，移项可得$4y=-13$，解得$y =-\frac{13}{4}$。
当$M(-1,0)$时，$P(-1,-1)$；当$M(1,0)$时：
设$P(1,y)$，$PM=-y$，$PB = 2$，$AB=-2 - y$。
根据勾股定理$PA^{2}=PB^{2}+AB^{2}=4+(-2 - y)^{2}$，因为$PA = PM$，所以$(-y)^{2}=4+(-2 - y)^{2}$。
展开得$y^{2}=4 + 4 + 4y+y^{2}$，移项可得$4y=-8$，解得$y=-2$。
所以表格依次填$-\frac{13}{4}$，$-1$，$-1$，$-2$。
3. （3）
设$P(x,y)$，$A(-1,-2)$，$M(x,0)$。
$PM=-y$，$PB=\vert x + 1\vert$，$AB=-2 - y$。
由$PA = PM$，根据勾股定理$PA^{2}=PB^{2}+AB^{2}$，即$(-y)^{2}=(x + 1)^{2}+(-2 - y)^{2}$。
展开：$y^{2}=x^{2}+2x + 1+4 + 4y+y^{2}$。
化简得$y=-\frac{1}{4}x^{2}-\frac{1}{2}x-\frac{5}{4}$。
4. （4）
对于二次函数$y =-\frac{1}{4}x^{2}-\frac{1}{2}x-\frac{5}{4}=-\frac{1}{4}(x^{2}+2x + 5)=-\frac{1}{4}(x + 1)^{2}-1$，其对称轴为$x=-1$，开口向下。
当$x=-1$时，$y_{max}=-1$。
当$x = 6$时，$y=-\frac{1}{4}\times6^{2}-\frac{1}{2}\times6-\frac{5}{4}=-\frac{36}{4}-\frac{12}{4}-\frac{5}{4}=-\frac{53}{4}$；当$x=-7$时，$y=-\frac{1}{4}\times(-7)^{2}-\frac{1}{2}\times(-7)-\frac{5}{4}=-\frac{49}{4}+\frac{14}{4}-\frac{5}{4}=-\frac{40}{4}=-10$。
因为$-\frac{53}{4}\lt - 10$，所以$y\leqslant - 1$。
5. （5）
设$P(x,y)$，$A(m,d)$，$M(x,0)$。
$PM=-y$，$PB=\vert x - m\vert$，$AB=-d - y$。
由$PA = PM$，根据勾股定理$PA^{2}=PB^{2}+AB^{2}$，即$(-y)^{2}=(x - m)^{2}+(-d - y)^{2}$。
展开：$y^{2}=x^{2}-2mx + m^{2}+d^{2}+2dy+y^{2}$。
化简得$y=-\frac{1}{2d}x^{2}+\frac{m}{d}x-\frac{m^{2}+d^{2}}{2d}$。
对于二次函数$y = ax^{2}+bx + c$（$a =-\frac{1}{2d}$，$b=\frac{m}{d}$，$c =-\frac{m^{2}+d^{2}}{2d}$），其对称轴为$x =-\frac{b}{2a}=m$。
当$x = m$时，$y=-\frac{1}{2d}\times m^{2}+\frac{m}{d}\times m-\frac{m^{2}+d^{2}}{2d}=\frac{-m^{2}+2m^{2}-m^{2}-d^{2}}{2d}=-\frac{d}{2}$。
所以曲线$L$的最高点坐标为$(m,-\frac{d}{2})$。
综上，答案依次为：（1）$(-1,-1)$；（2）$-\frac{13}{4}$，$-1$，$-1$，$-2$；（3）$y =-\frac{1}{4}x^{2}-\frac{1}{2}x-\frac{5}{4}$；（4）$y\leqslant - 1$；（5）$(m,-\frac{d}{2})$。