《2025年一本同步训练九年级数学上册人教版重庆专版》

12. [生活情境]为美化校园环境，某学校根据地形情况，要对景观带中一个长AD=4m、宽AB=1m的矩形水池ABCD进行加长改造(如图1，改造后的水池ABNM仍为矩形，以下简称水池1)，同时，再建造一个周长为12m的矩形水池EFGH(如图2，以下简称水池2).

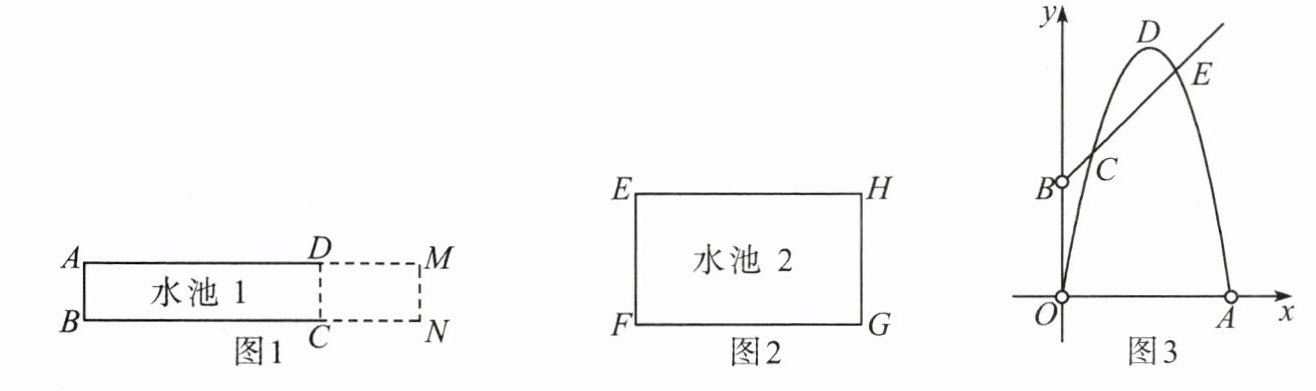
[建立模型]设水池ABCD的边AD加长的长度DM为x m(x＞0)，加长后水池1的总面积为y₁m²，则y₁关于x的函数解析式为y₁=x+4(x＞0).若水池2的边EF的长为x m(0＜x＜6)，面积为y₂m²，则y₂关于x的函数解析式为y₂=-x²+6x(0＜x＜6).上述两个函数在同一平面直角坐标系中的图象如图3所示.
[问题解决](1) 若水池2的面积随EF长度的增加而减小，则EF长度的取值范围是______，水池2面积的最大值是______m².
(2) 如图3，用字母标注的点中，表示两个水池面积相等的点是______，此时x的值是______.
(3) 当水池1的面积大于水池2的面积时，x的取值范围是__________________.
(4) 在1＜x＜4范围内，求水池1和水池2的面积差的最大值及此时x的值.
(5) 假设水池ABCD的边AD的长度为b m，其他条件不变(这个加长改造后的新水池简称水池3)，且水池3的总面积y₃m²，y₃关于x的函数解析式为y₃=x+b(x＞0).若水池3与水池2的面积相等时，x的值是唯一的，求b的值.

答案：
(1) $ 3 ＜ x ＜ 6 $ 9
(2) $ C $，$ E $ 1，4
(3) $ 0 ＜ x ＜ 1 $ 或 $ 4 ＜ x ＜ 6 $
(4) 水池 1 和水池 2 的面积差的最大值为 $ \frac{9}{4} $，此时 $ x $ 的值为 $ \frac{5}{2} $
(5) $ \frac{25}{4} $