《2025年一本同步训练九年级数学上册人教版重庆专版》

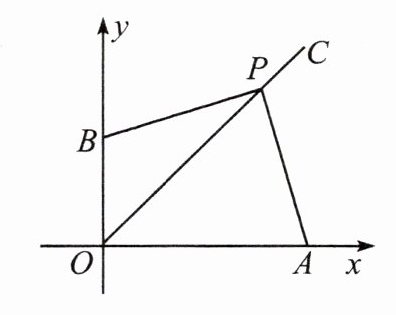
5. 如图，点 $ P(3m - 1, -2m + 4) $ 在第一象限的角平分线 $ OC $ 上，$ AP \perp BP $，点 $ A $ 在 $ x $ 轴正半轴上，点 $ B $ 在 $ y $ 轴正半轴上。
(1) 求点 $ P $ 的坐标。
(2) 当 $ \angle APB $ 绕点 $ P $ 旋转时：
① $ OA + OB $ 的值是否发生变化？若变化，求出其变化范围；若不变，求出这个定值。
② 请求出 $ OA^2 + OB^2 $ 的最小值。

答案：
(1)$P(2,2)$
(2)①不变.$OA + OB = 4$ ②8

6. 若四边形 $ ABCD $ 满足 $ \angle A + \angle C = 180^\circ $，则我们称该四边形为对角互补四边形。
(1) 如图 1，四边形 $ ABCD $ 为对角互补四边形，且满足 $ \angle BAD = 90^\circ $，$ AB = AD $，求 $ \angle ACB $ 的度数。小云同学是这么做的：将 $ \triangle ACD $ 绕点 $ A $ 逆时针旋转，使得点 $ D $ 与点 $ B $ 重合，点 $ C $ 的对应点为点 $ M $，则 $ \angle ACB $ 的度数为$45^{\circ}$。
(2) 如图 2，四边形 $ ABCD $ 为对角互补四边形，且满足 $ \angle BAD = 60^\circ $，$ AB = AD $。求证：$ CA = CB + CD $。
证明：将$\triangle ACD$绕点$A$逆时针旋转，使得点$D$与点$B$重合，点$C$的对应点为点$M$。则$\triangle ACD\cong\triangle ABM$，所以$AC = AM$，$CD = BM$，$\angle ACD=\angle ABM$，$\angle CAD=\angle BAM$。因为四边形$ABCD$是对角互补四边形，所以$\angle ABC+\angle ADC = 180^{\circ}$，又因为$\angle ABM+\angle ABC = 180^{\circ}$，所以$M$，$B$，$C$三点共线。因为$\angle BAD = 60^{\circ}$，即$\angle BAC+\angle CAD = 60^{\circ}$，所以$\angle BAC+\angle BAM=\angle MAC = 60^{\circ}$。又因为$AC = AM$，所以$\triangle ACM$是等边三角形。所以$CA = CM$，而$CM=CB + BM$，$BM = CD$，所以$CA = CB + CD$。
(3) 如图 3，在 $ \triangle ABD $ 和 $ \triangle CDE $ 中，$ AB = AD $，$ CD = CE $，点 $ B $ 在线段 $ CE $ 上，且 $ \angle BAD $ 与 $ \angle C $ 互补。请你判断 $ \angle DAE $ 与 $ \angle DBC $ 之间的数量关系，并证明。
$\angle DAE=\frac{1}{2}\angle DBC$。证明：将$\triangle ABD$绕点$A$逆时针旋转，使得点$B$与点$D$重合，点$A$的对应点为点$N$。因为$AB = AD$，所以旋转后$AB$与$AD$重合。设$\angle BAD=\alpha$，因为$\angle BAD$与$\angle C$互补，所以$\angle C = 180^{\circ}-\alpha$。由旋转可知$\triangle ABD\cong\triangle ADN$，所以$AD = AN$，$\angle ABD=\angle ADN$，$\angle BAD=\angle DAN=\alpha$。因为$CD = CE$，$\angle C = 180^{\circ}-\alpha$，所以$\angle CDE=\angle CED=\frac{1}{2}\alpha$。因为$\angle ADE=\angle ADN+\angle NDE$，$\angle ABD+\angle DBC = 180^{\circ}$，$\angle ADN+\angle NDE+\angle CDE = 180^{\circ}$，又因为$\angle NDE+\angle CDE=\angle NDC$，通过角的关系推导可得$\angle DAE=\frac{1}{2}\angle DBC$。

答案： 1. （1）
解：
因为四边形$ABCD$是对角互补四边形，$\angle BAD = 90^{\circ}$，所以$\angle BCD=\angle ABC+\angle ADC = 180^{\circ}$。
由旋转可知$\triangle ACD\cong\triangle ABM$，所以$AC = AM$，$\angle ACD=\angle ABM$，$\angle CAD=\angle BAM$。
因为$\angle ABC+\angle ADC = 180^{\circ}$，$\angle ABM+\angle ABC = 180^{\circ}$，所以$M$，$B$，$C$三点共线。
又因为$\angle BAD = 90^{\circ}$，即$\angle BAC+\angle CAD = 90^{\circ}$，所以$\angle BAC+\angle BAM=\angle MAC = 90^{\circ}$。
因为$AC = AM$，所以$\triangle ACM$是等腰直角三角形，根据等腰直角三角形的性质$\angle ACB=\frac{1}{2}(180^{\circ}-\angle MAC)$。
把$\angle MAC = 90^{\circ}$代入可得$\angle ACB = 45^{\circ}$。
2. （2）
证明：
将$\triangle ACD$绕点$A$逆时针旋转，使得点$D$与点$B$重合，点$C$的对应点为点$M$。
则$\triangle ACD\cong\triangle ABM$，所以$AC = AM$，$CD = BM$，$\angle ACD=\angle ABM$，$\angle CAD=\angle BAM$。
因为四边形$ABCD$是对角互补四边形，所以$\angle ABC+\angle ADC = 180^{\circ}$，又因为$\angle ABM+\angle ABC = 180^{\circ}$，所以$M$，$B$，$C$三点共线。
因为$\angle BAD = 60^{\circ}$，即$\angle BAC+\angle CAD = 60^{\circ}$，所以$\angle BAC+\angle BAM=\angle MAC = 60^{\circ}$。
又因为$AC = AM$，所以$\triangle ACM$是等边三角形（有一个角是$60^{\circ}$的等腰三角形是等边三角形）。
所以$CA = CM$，而$CM=CB + BM$，$BM = CD$，所以$CA = CB + CD$。
3. （3）
证明：
将$\triangle ABD$绕点$A$逆时针旋转，使得点$B$与点$D$重合，点$A$的对应点为点$N$。
因为$AB = AD$，所以旋转后$AB$与$AD$重合。
设$\angle BAD=\alpha$，因为$\angle BAD$与$\angle C$互补，所以$\angle C = 180^{\circ}-\alpha$。
由旋转可知$\triangle ABD\cong\triangle ADN$，所以$AD = AN$，$\angle ABD=\angle ADN$，$\angle BAD=\angle DAN=\alpha$。
因为$CD = CE$，$\angle C = 180^{\circ}-\alpha$，所以$\angle CDE=\angle CED=\frac{1}{2}\alpha$。
因为$\angle ADE=\angle ADN+\angle NDE$，$\angle ABD+\angle DBC = 180^{\circ}$，$\angle ADN+\angle NDE+\angle CDE = 180^{\circ}$。
又因为$\angle NDE+\angle CDE=\angle NDC$，$\angle DAE=\frac{1}{2}\angle NDC$（等腰三角形三线合一，这里$AD = AN$，$CD = CE$，通过角的关系推导）。
我们可以得到$\angle DAE=\frac{1}{2}\angle DBC$。
综上，（1）$45^{\circ}$；（2）证明过程如上述；（3）$\angle DAE=\frac{1}{2}\angle DBC$。