《2025年一本同步训练九年级数学上册人教版重庆专版》

10.【新考法·规律探究】如图,在平面直角坐标系中,将点$P(1,0)$向上平移$1$个单位长度得到点$P_{1}$,作点$P_{1}$关于原点的对称点$P_{2}$;将点$P_{2}$向上平移$2$个单位长度得到点$P_{3}$,作点$P_{3}$关于原点的对称点$P_{4}$;将点$P_{4}$向上平移$3$个单位长度得到点$P_{5}$,作点$P_{5}$关于原点的对称点$P_{6}$……那么点$P_{2026}$的坐标是____.

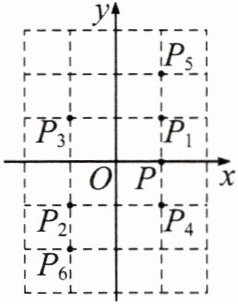
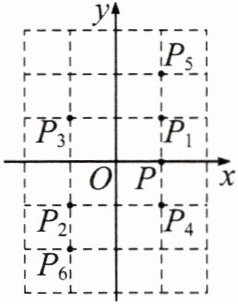
$(-1,-507)$

答案： $(-1,-507)$

11.如图,在平面直角坐标系中,已知点$A(2,-2)$,$P$是$x$轴上的一个动点.
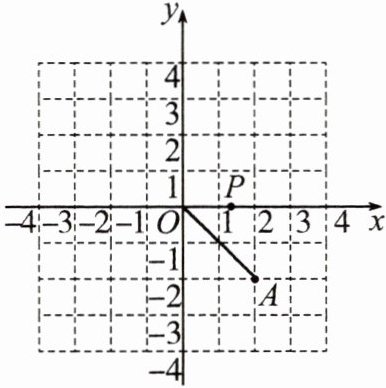
(1)若点$A_{1}$,$A_{2}$分别是点$A$关于原点的对称点和关于$y$轴的对称点,则点$A_{1}$的坐标为$(-2,2)$,点$A_{2}$的坐标为$(-2,-2)$,并在图中标出点$A_{1}$,$A_{2}$;
(2)求使$\triangle APO$是等腰三角形的点$P$的坐标.点$P$的坐标为$(2\sqrt{2},0)$，$(-2\sqrt{2},0)$，$(4,0)$，$(2,0)$

答案： 1. （1）
根据关于原点对称的点的坐标特征：若两点$(x,y)$与$(x',y')$关于原点对称，则$x'=-x$，$y'=-y$。
已知$A(2, - 2)$，所以$A_1$的坐标为$(-2,2)$。
根据关于$y$轴对称的点的坐标特征：若两点$(x,y)$与$(x',y')$关于$y$轴对称，则$x'=-x$，$y' = y$。
已知$A(2,-2)$，所以$A_2$的坐标为$(-2,-2)$。
2. （2）
设$P(x,0)$，已知$A(2,-2)$，$O(0,0)$。
根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$，则$OA=\sqrt{(2 - 0)^2+(-2 - 0)^2}=\sqrt{4 + 4}=\sqrt{8}=2\sqrt{2}$，$OP=\vert x\vert$，$AP=\sqrt{(x - 2)^2+(0 + 2)^2}=\sqrt{(x - 2)^2+4}$。
分三种情况讨论：
当$OA = OP$时**：
因为$OA = 2\sqrt{2}$，$OP=\vert x\vert$，所以$\vert x\vert=2\sqrt{2}$，解得$x = 2\sqrt{2}$或$x=-2\sqrt{2}$，此时$P_1(2\sqrt{2},0)$，$P_2(-2\sqrt{2},0)$。
当$OA = AP$时**：
因为$OA = 2\sqrt{2}$，$AP=\sqrt{(x - 2)^2+4}$，所以$\sqrt{(x - 2)^2+4}=2\sqrt{2}$。
两边平方得$(x - 2)^2+4 = 8$，即$(x - 2)^2=4$。
开方得$x - 2=\pm2$。
当$x - 2 = 2$时，$x = 4$；当$x - 2=-2$时，$x = 0$（$O$点与$P$点重合，舍去），此时$P_3(4,0)$。
当$OP = AP$时**：
因为$OP=\vert x\vert$，$AP=\sqrt{(x - 2)^2+4}$，所以$x^{2}=(x - 2)^2+4$。
展开$(x - 2)^2$得$x^{2}=x^{2}-4x + 4+4$。
移项得$x^{2}-x^{2}+4x=8$，即$4x = 8$，解得$x = 2$，此时$P_4(2,0)$。
综上，（1）$A_1(-2,2)$，$A_2(-2,-2)$；（2）点$P$的坐标为$(2\sqrt{2},0)$，$(-2\sqrt{2},0)$，$(4,0)$，$(2,0)$。

12.【新考法·新定义】年少的岁月里,约定是令人欣喜的!我们不妨约定:关于原点对称的一对点(不重合)称为一对“双子星”,图象至少经过一对“双子星”的函数称为“双子星函数”.
(1)若$A(\frac {5}{4-2s},-4)$和$B(-1,t^{2}-2t+1)$是一对“双子星”,则$s=$$-\frac {1}{2}$,$t=$3 或 -1.
(2)已知关于$x$的函数$y=kx+p$(其中$k$,$p$为常数)和“双子星函数”$y=x^{2}-3x-1$.
①求出“双子星函数”$y=x^{2}-3x-1$的图象上所有的“双子星”.
$(1,-3)$和$(-1,3)$
②关于$x$的函数$y=kx+p$的图象上是否存在“双子星”?如果有,指出共有多少对“双子星”;如果没有,请说明理由.
对于函数$y=kx+p$的图象,若$p=0$,则它有无数对“双子星”;若$p≠0$,则它没有“双子星”

答案：
(1)$-\frac {1}{2}$ 3 或 -1
(2)①$(1,-3)$和$(-1,3)$
②对于函数$y=kx+p$的图象,若$p=0$,则它有无数对“双子星”;若$p≠0$,则它没有“双子星”