《2025年一本同步训练九年级数学上册人教版重庆专版》

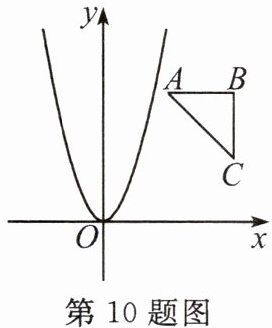
10. 如图，已知$Rt\triangle ABC$的顶点坐标分别为$A(1,2)$，$B(2,2)$，$C(2,1)$，若抛物线$y=ax^{2}(a＞0)$与该直角三角形无交点，则$a$的取值范围是（D）


A. $a＞2$
B. $0\lt a＜\frac {1}{4}$
C. $\frac {1}{4}≤a≤2$
D. $a＞2$或$0\lt a＜\frac {1}{4}$

答案： D

11. 如图，正方形$OABC$的面积为18，$OC$与$y$轴的正半轴的夹角为$15^{\circ }$，点$B$在抛物线$y=ax^{2}(a＞0)$的图象上，则$a$的值为____$\frac{1}{9}$.

答案： $ \frac{1}{9} $

12. 在平面直角坐标系中，已知点$A$在$y$轴正半轴上.

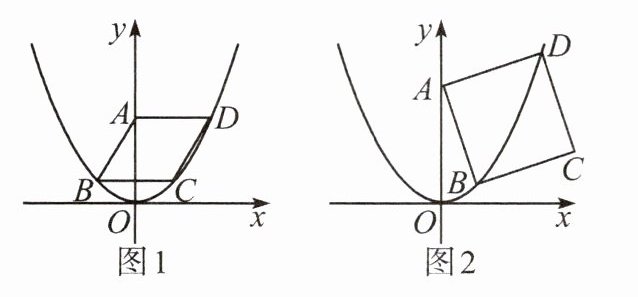
(1)如图1，已知菱形$ABCD$的顶点$B$，$C$，$D$在二次函数$y=x^{2}$的图象上，且$AD⊥y$轴，则菱形$ABCD$的边长为____.
(2)如图2，已知正方形$ABCD$的顶点$B$，$D$在二次函数$y=x^{2}$的图象上，点$B$，$D$在$y$轴的同侧，且点$B$在点$D$的左侧.设点$B$，$D$的横坐标分别为$m$，$n$，请探究$n-m$是否为定值，并说明理由.

答案： $(1)$求菱形$ABCD$的边长
已知$AD\perp y$轴，四边形$ABCD$是菱形，所以$AD = BC$，$AD// BC$，$AB = BC$。
因为$B$、$C$关于$y$轴对称，设$C$点坐标为$(a,a^{2})$（$a\gt0$），则$B$点坐标为$( - a,a^{2})$，$AD = BC = 2a$，$A$点坐标为$(0,a^{2})$，$D$点坐标为$(2a,a^{2})$。
又因为$D$点在$y = x^{2}$上，把$D(2a,a^{2})$代入$y = x^{2}$得：$a^{2}=(2a)^{2}$，即$a^{2}=4a^{2}$，$3a^{2}=0$（舍去）或者由菱形性质$AB = BC$，$AB$的长度为$\sqrt{(a - 0)^{2}+(a^{2}-a^{2})^{2}}=a$，$BC = 2a$，因为$AB = BC$，且$D$点$(2a,a^{2})$在$y=x^{2}$上，所以$a^{2}=(2a)^{2}$，$a = 0$（舍去），我们换一种思路，由于$BC$平行于$x$轴，$B$、$C$在$y = x^{2}$上，令$y = 1$，则$x=\pm1$，此时$BC = 2$，$AD = BC$，$AB = BC$，所以菱形$ABCD$的边长为$2$。
$(2)$判断$n - m$是否为定值
过点$B$作$BE\perp y$轴于点$E$，过点$D$作$DF\perp y$轴于点$F$。
因为四边形$ABCD$是正方形，所以$AB = AD$，$\angle BAD = 90^{\circ}$，则$\angle BAE+\angle DAF = 90^{\circ}$，又$\angle BAE+\angle ABE = 90^{\circ}$，所以$\angle ABE=\angle DAF$。
在$\triangle ABE$和$\triangle DAF$中，$\left\{\begin{array}{l}\angle AEB=\angle DFA = 90^{\circ}\\\angle ABE=\angle DAF\\AB = DA\end{array}\right.$，所以$\triangle ABE\cong\triangle DAF(AAS)$。
则$BE = AF$，$AE = DF$。
已知$B(m,m^{2})$，$D(n,n^{2})$，所以$BE=\vert m\vert=-m$（因为$m\lt0$），$DF = n$，$AE=n^{2}-m^{2}$，$AF = n^{2}-y_{A}$，$y_{A}=m^{2}+(-m)$。
因为$AE = DF$，所以$n^{2}-m^{2}=n$，又因为$BE = AF$，即$-m=n^{2}-(m^{2}-m)$，化简$\triangle ABE\cong\triangle DAF$得到的关系：
由$\triangle ABE\cong\triangle DAF$得$BE = AF$，$AE = DF$，即$\left\{\begin{array}{l}-m=n^{2}-y_{A}\\n^{2}-m^{2}=n\end{array}\right.$，消去$y_{A}$，将$y_{A}=m^{2}-m$代入不影响。
对$n^{2}-m^{2}=n + m$（平方差公式$n^{2}-m^{2}=(n + m)(n - m)$），因为$n\neq - m$（$B$，$D$在$y$轴同侧），所以$n - m = 1$，$n - m$是定值$1$。
综上，$(1)$菱形$ABCD$的边长为$\boldsymbol{2}$；$(2)$$n - m$是定值，$n - m=\boldsymbol{1}$。

13. 如图，二次函数$y=ax^{2}$的图象经过点$(1,\frac {1}{4})$，$P$是图象上的一点，过点$P$作$x$轴的垂线与直线$y=-1$交于点$M$.点$F(0,1)$在$y$轴上，直线$y=-1$与$y$轴交于点$H$.

(1)求二次函数的解析式；
(2)求证：$FM$平分$∠OFP$；
(3)当$\triangle FPM$是等边三角形时，求点$P$的坐标.

答案： 1. （1）求二次函数的解析式：
已知二次函数$y = ax^{2}$的图象经过点$(1,\frac{1}{4})$，将点$(1,\frac{1}{4})$代入$y = ax^{2}$中，可得$\frac{1}{4}=a\times1^{2}$，即$a = \frac{1}{4}$。
所以二次函数的解析式为$y=\frac{1}{4}x^{2}$。
2. （2）证明$FM$平分$\angle OFP$：
设点$P$的坐标为$(x,\frac{1}{4}x^{2})$，则点$M$的坐标为$(x, - 1)$。
根据两点间距离公式$d=\sqrt{(x_2 - x_1)^{2}+(y_2 - y_1)^{2}}$，可得$PF=\sqrt{x^{2}+(\frac{1}{4}x^{2}-1)^{2}}=\sqrt{x^{2}+\frac{1}{16}x^{4}-\frac{1}{2}x^{2}+1}=\sqrt{\frac{1}{16}x^{4}+\frac{1}{2}x^{2}+1}=\frac{1}{4}x^{2}+1$，$PM=\frac{1}{4}x^{2}+1$，所以$PF = PM$。
因为$PM\perp x$轴，$y=-1$与$x$轴平行，所以$\angle PMF=\angle MFH$。
又因为$PF = PM$，所以$\angle PFM=\angle PMF$，则$\angle PFM=\angle MFH$，即$FM$平分$\angle OFP$。
3. （3）当$\triangle FPM$是等边三角形时，求点$P$的坐标：
因为$\triangle FPM$是等边三角形，所以$\angle PMF = 60^{\circ}$，则$\angle MFH = 60^{\circ}$。
在$Rt\triangle FHM$中，$\tan\angle MFH=\frac{HM}{FH}$，已知$FH = 2$，$\tan60^{\circ}=\sqrt{3}$，所以$HM = 2\sqrt{3}$。
因为点$M$的坐标为$(x, - 1)$，所以$|x| = 2\sqrt{3}$。
当$x = 2\sqrt{3}$时，$y=\frac{1}{4}\times(2\sqrt{3})^{2}=3$；当$x=-2\sqrt{3}$时，$y=\frac{1}{4}\times(-2\sqrt{3})^{2}=3$。
所以点$P$的坐标为$(2\sqrt{3},3)$或$(-2\sqrt{3},3)$。