第44页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
1. 用绳子围成周长为10m的矩形,记矩形的一边长为x m,它的邻边长为y m,矩形的面积为S m²,当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是(
A. 一次函数关系、二次函数关系
B. 正比例函数关系、二次函数关系
C. 二次函数关系、一次函数关系
D. 正比例函数关系、一次函数关系
A
)A. 一次函数关系、二次函数关系
B. 正比例函数关系、二次函数关系
C. 二次函数关系、一次函数关系
D. 正比例函数关系、一次函数关系
答案:
A
2. (教材P52习题T4变式)已知一个直角三角形两条直角边的和是20cm,则这个直角三角形面积的最大值是(
A. 25cm²
B. 50cm²
C. 75cm²
D. 无法确定
B
)A. 25cm²
B. 50cm²
C. 75cm²
D. 无法确定
答案:
B
3. 如图,有一张矩形纸片ABCD,AD=16cm,AB=10cm.将该矩形纸片沿垂直于BC的三条虚线折成一个上下无盖的长方体纸盒,则长方体纸盒的最大容积为(
A. 80cm³
B. 160cm³
C. 320cm³
D. 640cm³
B
)A. 80cm³
B. 160cm³
C. 320cm³
D. 640cm³
答案:
B
4. 如图,正方形纸片ABCD的边长为4,将它剪去4个全等的直角三角形,得到四边形EFGH,则四边形EFGH面积的最小值为(
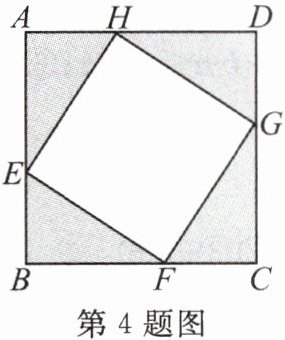
A. 6
B. 7
C. 8
D. 9
C
)
A. 6
B. 7
C. 8
D. 9
答案:
C
5. 某小区计划建一个矩形花圃,花圃的一边靠墙(墙长30m),另三边及中间的隔断用总长为88m的篱笆围成.如图,围成的花圃是矩形ABCD,并在边BC上留有两扇1m宽的门,则花圃的最大面积是
600
m².
答案:
600
6. 如图,已知□ABCD的周长为8cm,∠B=30°,设AB=x cm.
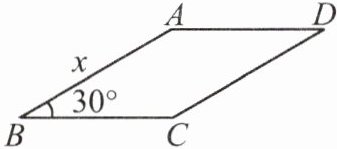
(1) □ABCD的面积y(cm²)关于x(cm)的函数解析式为
(2) 当x=

(1) □ABCD的面积y(cm²)关于x(cm)的函数解析式为
$ y = -\frac{1}{2}x^2 + 2x $
,自变量x的取值范围是$ 0 < x < 4 $
;(2) 当x=
2
时,y的值最大,最大值为2
.
答案:
(1) $ y = -\frac{1}{2}x^2 + 2x $ $ 0 < x < 4 $
(2) 2 2
(1) $ y = -\frac{1}{2}x^2 + 2x $ $ 0 < x < 4 $
(2) 2 2
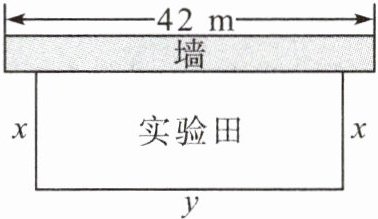
7. (2024·湖北)如图,某校劳动实践基地用总长为80m的栅栏围成一块一边靠墙的矩形实验田,墙长为42m.栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边的长为x(单位:m),与墙平行的一边的长为y(单位:m),面积为S(单位:m²).
(1) 直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围).
(2) 矩形实验田的面积S能达到750m²吗?如果能,求出x的值;如果不能,请说明理由.
(3) 当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
(1) 直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围).
(2) 矩形实验田的面积S能达到750m²吗?如果能,求出x的值;如果不能,请说明理由.
(3) 当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?

答案:
(1) $ y = -2x + 80 $,$ S = -2x^2 + 80x $
(2) 能. 当 $ x = 25m $ 时,矩形实验田的面积 $ S $ 能达到 $ 750m^2 $
(3) 当 $ x = 20m $ 时,$ S $ 有最大值,最大值为 $ 800m^2 $
(1) $ y = -2x + 80 $,$ S = -2x^2 + 80x $
(2) 能. 当 $ x = 25m $ 时,矩形实验田的面积 $ S $ 能达到 $ 750m^2 $
(3) 当 $ x = 20m $ 时,$ S $ 有最大值,最大值为 $ 800m^2 $
查看更多完整答案,请扫码查看


