《2025年一本同步训练九年级数学上册人教版重庆专版》

16. (2024·烟台)每年5月的第三个星期日为全国助残日，今年的主题是“科技助残，共享美好生活”.康宁公司计划在该月销售一批新研发的便携式轮椅，根据市场调查发现，当每辆轮椅盈利200元时，每天可售出60辆.单价每降低10元，每天可多售出4辆.公司决定在成本不变的情况下降价销售，但每辆轮椅的利润不低于180元.设每辆轮椅降价$x$元，每天的销售利润为$y$元.
(1)求$y$与$x$之间的函数解析式.每辆轮椅降价多少元时，每天的销售利润最大？最大利润为多少元？
(2)全国助残日当天，公司共获得销售利润12160元，请问这天售出了多少辆轮椅？

答案： 16.
(1)$y=-\frac {2}{5}x^{2}+20x+12000$，每辆轮椅降价20元时，每天的销售利润最大，最大利润为12240元
(2)64辆

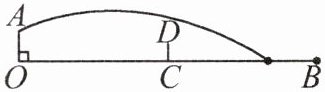
17. 乒乓球被誉为中国国球.乒乓球台的截面示意图如图所示，一名运动员从球台边缘正上方以击球高度$OA$为28.75cm的高度，将乒乓球向正前方击打到对面球台，乒乓球的运行路线近似看作抛物线的一部分.乒乓球到球台的竖直高度记为$y$(单位：$cm$)，乒乓球运行过程中到起始点的水平距离记为$x$(单位：$cm$).测得如下数据：
| 水平距离$x/cm$ | 0 | 10 | 50 | 90 | 130 | 170 | 230 |
| --- | --- | --- | --- | --- | --- | --- | --- |
| 竖直高度$y/cm$ | 28.75 | 33 | 45 | 49 | 45 | 33 | 0 |
(1)①当乒乓球到达最高点时，到球台的竖直高度是49$cm$，当乒乓球落在对面球台上时，到起始点的水平距离是230$cm$；
②求满足条件的抛物线的函数解析式.
②$y=-0.0025(x-90)^{2}+49$
(2)技术分析：如果只上下调整击球高度$OA$，乒乓球的运行轨迹形状不变，那么为了确保乒乓球既能过网，又能落在对面球台上，需要计算出$OA$的取值范围，以利于有针对性地训练.乒乓球台长$OB$为274cm，球网高$CD$为15.25cm，现在已经计算出乒乓球恰好过网的击球离度$OA$的值约为1.27cm.请你计算出乒乓球恰好落在对面球台边缘点$B$处时，击球高度$OA$的值(乒乓球大小忽略不计).
64.39cm

答案： 17.
(1)①49 230 ②$y=-0.0025(x-90)^{2}+49$
(2)64.39cm