《2025年一本同步训练九年级数学上册人教版重庆专版》

10.如图,线段$AB=5$,动点P以每秒1个单位长度的速度从点B出发,沿线段BA运动至点A.以线段AP为边作正方形APCD,以线段PB的长为半径作圆.设点P的运动时间为$t(0≤t≤5)$,正方形APCD的周长为y,圆B的面积为S,则S与t,y与t满足的函数关系分别是 (C)
A.一次函数关系、二次函数关系
B.正比例函数关系、二次函数关系
C.二次函数关系、一次函数关系
D.二次函数关系、正比例函数关系

答案： C

11.如图,在四边形ABCD中,$AC⊥BD,AC+BD=10$,M和N分别是BD和AC的中点,连接AM,MN,DN,BA和CD的延长线交于点P,连接PM,PN.设$S_{△PMN}=y,AC=x$,则y关于x的函数解析式为____.(不必写出x的取值范围)

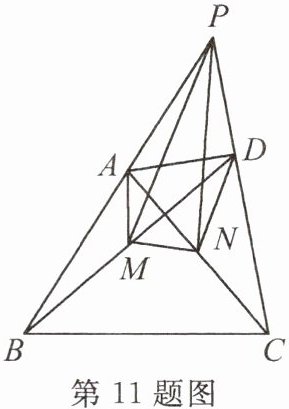
$y = -\frac{1}{8}x^{2} + \frac{5}{4}x$

答案： $y = -\frac{1}{8}x^{2} + \frac{5}{4}x$

12.一家用电器开发公司研制出一种新型的电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销售量,公司决定采取降价的办法,经市场调研发现:每降价1元,月销售量可增加2万件.
(1)求出月销售量y(万件)关于销售单价x(元)的函数解析式(不必写出x的取值范围);
(2)求出月销售利润z(万元)关于销售单价x(元)的函数解析式(不必写出x的取值范围);
(3)若某月的利润为350万元,则该月的销售量和销售单价分别为多少?

答案：
(1)$y = -2x + 100$
(2)$z = -2x^{2} + 136x - 1800$
(3)该月的销售量为 50 万件，销售单价为 25 元

13.如图,在矩形ABCD中,$AB=6cm,BC=12cm$,边AB上的动点E从点B出发,以1cm/s的速度向点A运动,到点A停止运动;同时边BC上的动点F从点B出发,以2cm/s的速度向点C运动,到点C停止运动.设动点运动的时间为t s,$△DEF$的面积为$S cm^{2}$.
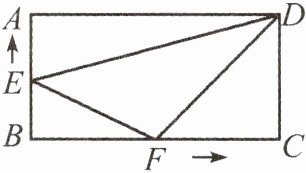
(1)求S关于t的函数解析式,并求出t的取值范围;
(2)当$△DEF$是直角三角形时,求$△DEF$的面积.

答案：
(1)$S = -t^{2} + 12t$，$0 ＜ t \leq 6$
(2)$36cm^{2}$ 或 $\frac{135}{4}cm^{2}$