《2025年一本同步训练九年级数学上册人教版重庆专版》

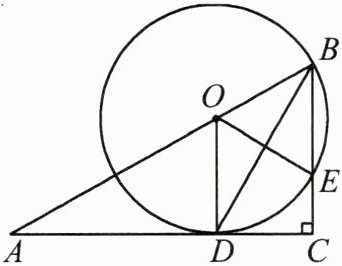
9.如图,在$Rt△ABC$中,$∠C=90^{\circ }$,BD是$∠ABC$的平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E,连接OD,OE.
(1)求证:$OD⊥AC;$
(2)若$OB=8,CD=4\sqrt {3}$,求四边形ODCE的面积.

答案： 解:
(1)证明:
∵BD平分∠ABC,
∴∠ABD=∠CBD.
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODB=∠CBD,
∴OD//BC,
∴∠ODC+∠C=180°.
∵∠C=90°,
∴∠ODC=90°,
∴OD⊥AC.
(2)24√3

10.如图,AB为半圆的直径,点O为圆心,$OC⊥AB$交半圆于点C,D是半圆上的动点(不与点A,B,C重合),点D从点A出发向点B运动,过点D作$DE⊥AB,DF⊥OC$,垂足分别为E,F,分别取DE和DF的中点M,N,连接MN.若$AB=10$,则下列关于MN的说法正确的是 (D)
A.先变大后变小
B.先变小后变大
C.等于5
D.等于2.5

答案： D

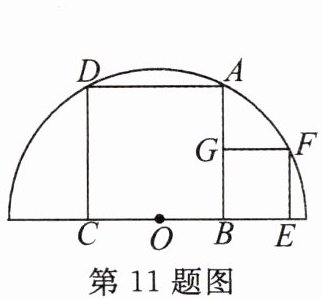
11.如图,两个正方形彼此相邻,且大正方形ABCD的顶点A,D在半圆O上,小正方形BEFG的顶点F在半圆O上,B,E两点在半圆O的直径上,点G在大正方形的边AB上.若小正方形的边长为4 cm,则该圆的半径为______cm.

4√5

答案： 4√5

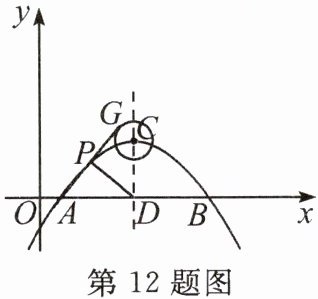
12.如图,已知抛物线$y=-\frac {3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,$\odot C$的半径为1,G为$\odot C$上的一动点,P为AG的中点,则DP的最大值为______3.

答案： 3

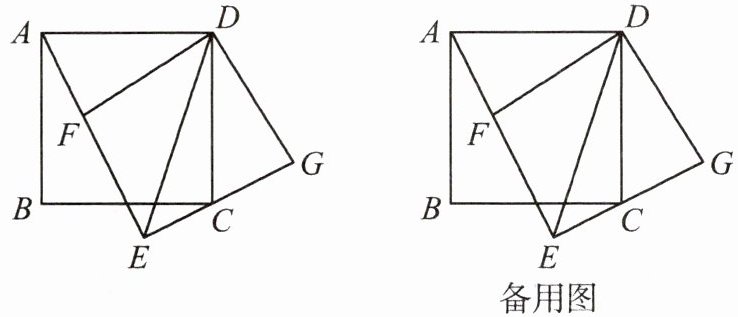
13.如图,正方形ABCD的边长为2,F为其内部的一点,且点F与点B之间的距离为1.将$△ADF$绕点D逆时针旋转$90^{\circ }$得到$△CDG$,AF,GC的延长线交于点E,连接DE.
(1)判断AF与GC之间的位置关系,并说明理由;
(2)求证:$EF+EG=\sqrt {2}DE;$
(3)直接写出A,G两点间的最短距离.

答案： $(1)$ 判断$AF$与$GC$之间的位置关系
解：$AF\perp GC$。
理由如下：
因为将$\triangle ADF$绕点$D$逆时针旋转$90^{\circ}$得到$\triangle CDG$，
所以$\triangle ADF\cong\triangle CDG$，则$\angle DAF = \angle DCG$。
在正方形$ABCD$中，$\angle DAB+\angle ABC = 90^{\circ}+90^{\circ}=180^{\circ}$，$\angle DAB=\angle DAF + \angle FAB$，
$\angle DCG+\angle FAB=\angle DAF+\angle FAB = 90^{\circ}$。
在$\triangle ABE$中，$\angle AEB=180^{\circ}-(\angle FAB + \angle ABC+\angle DCG)=180^{\circ}-(90^{\circ}+ 90^{\circ}) = 90^{\circ}$，所以$AF\perp GC$。
$(2)$ 证明$EF + EG=\sqrt{2}DE$
证明：过点$D$作$DH\perp DE$交$EA$的延长线于$H$。
因为$\triangle ADF$绕点$D$逆时针旋转$90^{\circ}$得到$\triangle CDG$，所以$DF = DG$，$\angle FDG = 90^{\circ}$。
又因为$\angle HDE=\angle FDG = 90^{\circ}$，所以$\angle HDF+\angle FDE=\angle EDG+\angle FDE$，即$\angle HDF=\angle EDG$。
由$(1)$知$\angle DAF=\angle DCG$，$\angle DAF+\angle DAH = 180^{\circ}$，$\angle DCG+\angle ECG = 180^{\circ}$，所以$\angle DAH=\angle ECG$。
因为$\angle AEB = 90^{\circ}$，$\angle DCE = 90^{\circ}$，所以$\angle AFD+\angle DAF=\angle DGC+\angle DCG = 90^{\circ}$，又$\angle DAF=\angle DCG$，$\angle AFD=\angle DGC$，$\angle AFD=\angle HFD$（对顶角相等），$\angle DGC=\angle DGE$（对顶角相等），所以$\angle HFD=\angle DGE$。
在$\triangle HDF$和$\triangle EDG$中：
$\begin{cases}\angle HDF=\angle EDG\\DF = DG\\\angle HFD=\angle DGE\end{cases}$
所以$\triangle HDF\cong\triangle EDG(ASA)$，则$HF = EG$，$DH = DE$。
因为$\angle HDE = 90^{\circ}$，$DH = DE$，所以$\triangle HDE$是等腰直角三角形，根据等腰直角三角形三边关系$a:a:\sqrt{2}a$（$a$为直角边），则$HE=\sqrt{2}DE$。
又因为$HE=HF + EF$，$HF = EG$，所以$EF + EG=\sqrt{2}DE$。
$(3)$ 求$A$，$G$两点间的最短距离
因为点$F$与点$B$之间的距离为$1$，所以点$F$在以$B$为圆心，$1$为半径的圆上。
由旋转性质知$DG = DF$，$AD = CD = 2$，$\angle ADC = 90^{\circ}$，$\angle FDG = 90^{\circ}$。
$AG$的最小值为$AD - DG$的最小值，$DG = DF$，$DF$的最小值为$BD - 1$（当$B$，$F$，$D$共线时，$DF$最小）。
在正方形$ABCD$中，$BD=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$，$DF_{\min}=2\sqrt{2}-1$，$DG = DF$，所以$AG_{\min}=AD - DG_{\min}=2-(2\sqrt{2}-1)=3 - 2\sqrt{2}$。
综上，答案依次为：$(1)$$\boldsymbol{AF\perp GC}$；$(2)$见上述证明过程；$(3)$$\boldsymbol{3 - 2\sqrt{2}}$。