《2025年一本同步训练九年级数学上册人教版重庆专版》

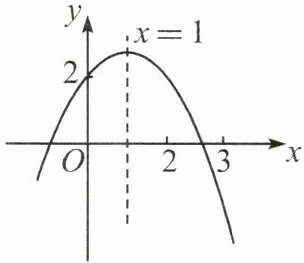
2.（2024·泰安）二次函数$y = ax^{2}+bx + c(a\neq0)$的部分图象如图所示，该函数图象的对称轴是$x = 1$，图象与$y$轴交点的纵坐标是2.有下列结论：①$2a + b = 0$；②方程$ax^{2}+bx + c = 0$一定有一个根在$-2$和$-1$之间；③方程$ax^{2}+bx + c-\frac{3}{2}=0$一定有两个不等的实数根；④$b - a＜2$.其中正确结论的个数为（B）

A.1
B.2
C.3
D.4

答案： B

3.（2024·遂宁）如图，已知抛物线$y = ax^{2}+bx + c$（$a$，$b$，$c$为常数，且$a\neq0$）的对称轴为$x = -1$，且该抛物线与$x$轴交于点$A(1,0)$，与$y$轴的交点$B$在$(0,-2)$，$(0,-3)$之间（不含端点），则下列结论正确的有（B）
①$abc＞0$；②$9a - 3b + c\geqslant0$；③$\frac{2}{3}＜a＜1$；④若方程$ax^{2}+bx + c = x + 1$的两根为$m$，$n(m＜n)$，则$-3＜m＜1＜n$.

A.1个
B.2个
C.3个
D.4个

答案： B

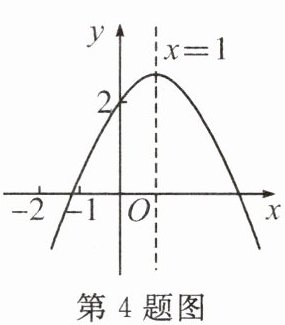
4.已知二次函数$y = ax^{2}+bx + c(a\neq0)$的图象如图所示.有下列结论：①$abc＞0$；②$(a + c)^{2}＞b^{2}$；③$4ac - b^{2}＜0$；④$1＜2b$；⑤$m(am + b)＜a + b(m\neq1)$.其中正确的结论有（D）

A.1个
B.2个
C.3个
D.4个

答案： D

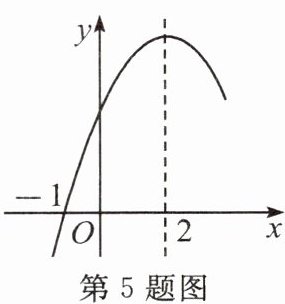
5.（2024·日照）已知二次函数$y = ax^{2}+bx + c(a\neq0)$图象的一部分如图所示，该函数图象经过点$(-1,0)$，对称轴为$x = 2$.有下列结论：①$abc＜0$；②$a + c = b$；③多项式$ax^{2}+bx + c$可因式分解为$(x + 1)(x - 5)$；④当$m＞-9a$时，关于$x$的方程$ax^{2}+bx + c = m$无实数根.其中正确的结论有（C）

A.1个
B.2个
C.3个
D.4个

答案： C

6.（2025·九龙坡区月考）抛物线$y = ax^{2}+bx + c(a\neq0)$的部分图象如图所示，对称轴为$x = -2$.有下列说法：①$abc＞0$；②$c-\frac{3}{4}b＜0$；③$4a^{2}-2ab\geqslant at(at + b)$（$t$为全体实数）；④若图象上存在点$A(x_{1},y_{1})$和点$B(x_{2},y_{2})$，当$n＜x_{1}＜x_{2}＜n + 5$时，满足$y_{1}=y_{2}$，则$n$的取值范围是$-7＜n＜-2$.其中正确的有（①③④）
A.1个
B.2个
C.3个
D.4个

答案： 1. 首先分析$a$，$b$，$c$的正负性：
由抛物线开口向下，得$a\lt0$。
对称轴$x =-\frac{b}{2a}=-2$，则$b = 4a\lt0$。
由抛物线与$y$轴交点在$y$轴正半轴，得$c\gt0$。
所以$abc\gt0$，故①正确。
2. 然后看$c-\frac{3}{4}b$：
当$x=-4$时，$y = 16a-4b + c\lt0$，又$b = 4a$，则$16a-4\times4a + c=c\lt0$（错误，这里换一种方法）。
对称轴$x=-2$，当$x = 0$与$x=-4$时$y$值相等，$y(0)=c$，$y(-4)=16a - 4b + c$，$b = 4a$，$y(-4)=c$，$y(-3)=9a-3b + c$，$b = 4a$，$y(-3)=9a-12a + c=c - 3a$，因为$a\lt0$，$c\gt0$，$y(-3)\gt0$。
当$x=-1$时，$y=a - b + c$，$b = 4a$，$y=a-4a + c=c - 3a$，$y(-1)=c - 3a\gt0$。
当$x=-2$时，$y = 4a-2b + c$，$b = 4a$，$y = 4a-8a + c=c - 4a$，因为$a\lt0$，$y(-2)=c - 4a\gt0$。
由对称轴$x=-2$，$y = ax^{2}+bx + c=a(x + 2)^{2}+k$（$k$为顶点纵坐标），$y=ax^{2}+4ax + c$，当$x=-1$时，$y=a-4a + c=c - 3a$，当$x = 0$时，$y=c$，当$x=-3$时，$y = 9a-12a + c=c - 3a$。
当$x=-2$时，$y = 4a-8a + c=c - 4a$。
因为$x=-1$与$x=-3$关于$x=-2$对称，$y(-1)=y(-3)=c - 3a\gt0$，$b = 4a$，$c-\frac{3}{4}b=c - 3a\gt0$，故②错误。
3. 接着看$4a^{2}-2ab\geqslant at(at + b)$：
当$x=-2$时，$y$有最大值$y = 4a-2b + c$。
对于任意实数$t$，$ax^{2}+bx + c\leqslant4a-2b + c$（当$x=-2$时取等号），即$ax^{2}+bx\leqslant4a - 2b$，令$x = t$，则$at^{2}+bt\leqslant4a - 2b$，$4a^{2}-2ab-(at^{2}+bt)=4a^{2}-2ab - at^{2}-bt=a(4a - t^{2})-b(2a + t)$，因为$b = 4a$，$4a^{2}-2ab-(at^{2}+bt)=4a^{2}-8a^{2}-at^{2}-4at=-4a^{2}-at^{2}-4at=-a(4a + t^{2}+4t)=-a(t + 2)^{2}$，又$a\lt0$，所以$-a(t + 2)^{2}\geqslant0$，即$4a^{2}-2ab\geqslant at(at + b)$（$t$为全体实数），故③正确。
4. 最后看$n$的取值范围：
因为对称轴$x=-2$，$\vert x_{1}-(-2)\vert=\vert x_{2}-(-2)\vert$，$x_{2}-(-2)=- (x_{1}-(-2))$，$x_{1}+x_{2}=-4$。
又$n\lt x_{1}\lt x_{2}\lt n + 5$，$\left\{\begin{array}{l}n\lt - 2\\n + 5\gt - 2\end{array}\right.$（$x_{1}\lt x_{2}$，对称轴$x=-2$），解$n + 5\gt - 2$得$n\gt - 7$，解$n\lt - 2$得$n\lt - 2$，所以$-7\lt n\lt - 2$，故④正确。
综上，①③④正确，正确的有$3$个，答案是C。

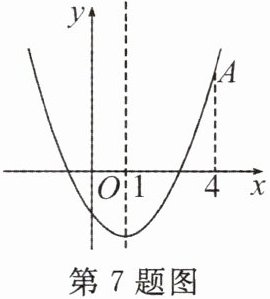
7.二次函数$y = ax^{2}+bx + c(a\neq0)$的大致图象如图所示，顶点坐标为$(1,-4a)$，$A(4,y_{1})$是该抛物线上的一点.若$D(x_{2},y_{2})$是抛物线上任意一点，有下列结论：①$4a - 2b + c＞0$；②若$y_{2}＞y_{1}$，则$x_{2}＞4$；③$3a + c = 0$；④若方程$a(x + 1)(x - 3)=-1$有两个实数根$n_{1}$和$n_{2}$，且$n_{1}＜n_{2}$，则$-1＜n_{1}＜n_{2}＜3$；⑤$m$为任意实数，则$m(am + b)\geqslant-4a - c$.其中正确的结论有（D）

A.1个
B.2个
C.3个
D.4个

答案： D

8.如图，抛物线$y = ax^{2}+bx + c$与$x$轴正半轴交于$A$，$B$两点，点$A$的坐标为$(1,0)$，点$B$的坐标为$(5,0)$.有下列结论：①$abc＜0$；②$2a + b＞0$；③$a + 4c＜0$；④当$0\leqslant x\leqslant4$时，$c\leqslant y\leqslant16a + 4b + c$；⑤对于任意的实数$m$，均有$am^{2}+bm\leqslant-9a$；⑥若$m＜0$，则关于$x$的方程$a|x|^{2}+b|x|+c = m$一定有4个实数根.其中正确的有（B）
A.②③⑤
B.②③⑤⑥
C.①④⑥
D.②③⑥

答案： 1. 首先，根据抛物线与$x$轴交点坐标求对称轴：
已知抛物线$y = ax^{2}+bx + c$与$x$轴交于$A(1,0)$，$B(5,0)$，根据对称轴公式$x =-\frac{b}{2a}=\frac{1 + 5}{2}=3$，则$b=-6a$。
由抛物线开口向下，得$a\lt0$，所以$b=-6a\gt0$。
由抛物线与$y$轴负半轴相交，得$c\lt0$。
2. 然后，判断①：
因为$a\lt0$，$b\gt0$，$c\lt0$，所以$abc\gt0$，故①**错误**。
3. 接着，判断②：
对于$2a + b$，把$b=-6a$代入得$2a + b=2a-6a=-4a$，因为$a\lt0$，所以$-4a\gt0$，即$2a + b\gt0$，故②**正确**。
4. 再判断③：
当$x = 1$时，$y=a + b + c = 0$，把$b=-6a$代入得$a-6a + c = 0$，则$c = 5a$。
所以$a + 4c=a + 20a=21a$，又$a\lt0$，所以$a + 4c\lt0$，故③**正确**。
5. 再判断④：
对称轴$x = 3$，当$x = 3$时，$y$有最大值$y = 9a+3b + c$，把$b=-6a$代入得$y = 9a-18a + c=-9a + c$。
当$x = 0$时，$y = c$；当$x = 4$时，$y = 16a + 4b + c=16a-24a + c=-8a + c$。
因为$a\lt0$，$-9a + c\gt-8a + c$，所以当$0\leqslant x\leqslant4$时，$c\leqslant y\leqslant-9a + c$，故④**错误**。
6. 再判断⑤：
当$x = 3$时，$y$有最大值$y = 9a + 3b + c$，当$x=m$时，$y = am^{2}+bm + c$。
因为$y_{max}=9a + 3b + c$，$b=-6a$，$c = 5a$，$y_{max}=9a-18a + 5a=-4a$。
$am^{2}+bm + c\leqslant9a + 3b + c$，即$am^{2}+bm\leqslant9a + 3b$，把$b=-6a$代入得$am^{2}+bm\leqslant9a-18a=-9a$，故⑤**正确**。
7. 最后，判断⑥：
令$t=\vert x\vert$，则方程$a\vert x\vert^{2}+b\vert x\vert + c = m$化为$at^{2}+bt + c - m = 0$（$t\geqslant0$）。
因为$m\lt0$，$\Delta=b^{2}-4a(c - m)=b^{2}-4ac + 4am$，$b=-6a$，$c = 5a$，$\Delta = 36a^{2}-20a^{2}+4am=16a^{2}+4am$。
又$a\lt0$，$m\lt0$，所以$\Delta\gt0$，且$y = at^{2}+bt + c - m$（$a\lt0$），当$t = 0$时，$y=c - m$，$c\lt0$，$m\lt0$，$c - m\lt0$，所以$at^{2}+bt + c - m = 0$有两个正根$t_{1}$，$t_{2}$（$t_{1}\neq t_{2}$），则$\vert x\vert=t_{1}$，$\vert x\vert=t_{2}$，所以$x=\pm t_{1}$，$x=\pm t_{2}$，方程$a\vert x\vert^{2}+b\vert x\vert + c = m$一定有$4$个实数根，故⑥**正确**。
综上，②③⑤⑥正确，答案是B。