第69页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
9. 如图所示,在$\triangle ABC$中,$\angle ABC = 45^{\circ}$,$AD\perp BC$于点$D$,$BE\perp AC$于点$E$,交$AD$于点$F$,将线段$AC$绕点$C$逆时针旋转$90^{\circ}$得到线段$GC$,连接$BG$。
(1)求证:$BF = AC$;
(2)若$AC=\sqrt{5}$,$BD = 2CD$,求线段$BG$的长。

(1)求证:$BF = AC$;
(2)若$AC=\sqrt{5}$,$BD = 2CD$,求线段$BG$的长。

答案:
1. (1)证明:
因为$AD\perp BC$,$BE\perp AC$,所以$\angle BDF=\angle ADC = 90^{\circ}$,$\angle BEC=\angle ADC = 90^{\circ}$。
又因为$\angle BFD=\angle AFE$(对顶角相等),根据三角形内角和为$180^{\circ}$,可得$\angle DBF=\angle DAC$。
已知$\angle ABC = 45^{\circ}$,$\angle ADB = 90^{\circ}$,所以$\triangle ABD$是等腰直角三角形,那么$AD = BD$。
在$\triangle BDF$和$\triangle ADC$中:
$\left\{\begin{array}{l}\angle BDF=\angle ADC\\BD = AD\\\angle DBF=\angle DAC\end{array}\right.$
根据$ASA$(角 - 边 - 角)定理,可得$\triangle BDF\cong\triangle ADC$。
所以$BF = AC$。
2. (2)解:
设$CD=x$,因为$BD = 2CD$,所以$BD = 2x$。
由(1)知$\triangle ABD$是等腰直角三角形,$AD = BD = 2x$,$AC=\sqrt{5}$,在$Rt\triangle ADC$中,根据勾股定理$AC^{2}=AD^{2}+CD^{2}$,即$(\sqrt{5})^{2}=(2x)^{2}+x^{2}$。
化简得$5 = 4x^{2}+x^{2}$,也就是$5x^{2}=5$,解得$x = 1$($x=-1$舍去)。
所以$CD = 1$,$BD = 2$,$BC=BD + CD=3$。
因为线段$AC$绕点$C$逆时针旋转$90^{\circ}$得到线段$GC$,所以$AC = GC=\sqrt{5}$,$\angle ACG = 90^{\circ}$。
又因为$\triangle BDF\cong\triangle ADC$,所以$BF = AC$,$AC = GC$,则$BF = GC$。
因为$\angle BCG=\angle BCA+\angle ACG$,$\angle BFD=\angle AFE$,$\angle AEF=\angle ADC = 90^{\circ}$,可得$\angle FBD=\angle CAD$,$\angle BCA+\angle CAD = 90^{\circ}$,$\angle ACG = 90^{\circ}$,所以$\angle FBD+\angle BCA+\angle ACG=\angle BCG+\angle FBD=90^{\circ}+\angle BCA+\angle FBD$,又因为$\angle FBD=\angle CAD$,$\angle BCA+\angle CAD = 90^{\circ}$,所以$\angle BCG+\angle FBD = 180^{\circ}-\angle BEC=90^{\circ}$($\angle BEC = 90^{\circ}$),$\angle BCG = 90^{\circ}+\angle BCA$,$\angle FBD+\angle BCA = 90^{\circ}$,所以$\angle FBC+\angle BCG=90^{\circ}$($\angle FBC=\angle FBD$),$\angle BCG = 90^{\circ}+\angle BCA$,$\angle FBC+\angle BCA = 90^{\circ}$,$\angle FBC+\angle BCG=\angle FBC + 90^{\circ}+\angle BCA=180^{\circ}$,$\angle BCG-\angle BCA = 90^{\circ}$,$\angle FBC=\angle BCA$(由$\triangle BDF\cong\triangle ADC$)不成立,重新分析:
因为$\angle ACG = 90^{\circ}$,$\angle BCD$为锐角,$\angle BCG=\angle BCD + 90^{\circ}$,$\triangle BDF\cong\triangle ADC$,$BF = AC$,$AC = GC$,所以$BF = GC$。
过$G$作$GH\perp BC$交$BC$延长线于$H$。
因为$\angle ACG = 90^{\circ}$,$\angle ADC = 90^{\circ}$,$\angle ACD+\angle HCG=90^{\circ}$,$\angle ACD+\angle CAD = 90^{\circ}$,所以$\angle CAD=\angle HCG$。
又$AC = GC$,$\angle ADC=\angle H = 90^{\circ}$,所以$\triangle ADC\cong\triangle CHG(AAS)$。
则$CH = AD = 2$,$GH = CD = 1$。
$BH=BC + CH=3 + 2=5$。
在$Rt\triangle BGH$中,根据勾股定理$BG=\sqrt{BH^{2}+GH^{2}}$。
把$BH = 5$,$GH = 1$代入可得$BG=\sqrt{5^{2}+1^{2}}=\sqrt{25 + 1}=\sqrt{26}$。
综上,(1)得证$BF = AC$;(2)$BG$的长为$\sqrt{26}$。
因为$AD\perp BC$,$BE\perp AC$,所以$\angle BDF=\angle ADC = 90^{\circ}$,$\angle BEC=\angle ADC = 90^{\circ}$。
又因为$\angle BFD=\angle AFE$(对顶角相等),根据三角形内角和为$180^{\circ}$,可得$\angle DBF=\angle DAC$。
已知$\angle ABC = 45^{\circ}$,$\angle ADB = 90^{\circ}$,所以$\triangle ABD$是等腰直角三角形,那么$AD = BD$。
在$\triangle BDF$和$\triangle ADC$中:
$\left\{\begin{array}{l}\angle BDF=\angle ADC\\BD = AD\\\angle DBF=\angle DAC\end{array}\right.$
根据$ASA$(角 - 边 - 角)定理,可得$\triangle BDF\cong\triangle ADC$。
所以$BF = AC$。
2. (2)解:
设$CD=x$,因为$BD = 2CD$,所以$BD = 2x$。
由(1)知$\triangle ABD$是等腰直角三角形,$AD = BD = 2x$,$AC=\sqrt{5}$,在$Rt\triangle ADC$中,根据勾股定理$AC^{2}=AD^{2}+CD^{2}$,即$(\sqrt{5})^{2}=(2x)^{2}+x^{2}$。
化简得$5 = 4x^{2}+x^{2}$,也就是$5x^{2}=5$,解得$x = 1$($x=-1$舍去)。
所以$CD = 1$,$BD = 2$,$BC=BD + CD=3$。
因为线段$AC$绕点$C$逆时针旋转$90^{\circ}$得到线段$GC$,所以$AC = GC=\sqrt{5}$,$\angle ACG = 90^{\circ}$。
又因为$\triangle BDF\cong\triangle ADC$,所以$BF = AC$,$AC = GC$,则$BF = GC$。
因为$\angle BCG=\angle BCA+\angle ACG$,$\angle BFD=\angle AFE$,$\angle AEF=\angle ADC = 90^{\circ}$,可得$\angle FBD=\angle CAD$,$\angle BCA+\angle CAD = 90^{\circ}$,$\angle ACG = 90^{\circ}$,所以$\angle FBD+\angle BCA+\angle ACG=\angle BCG+\angle FBD=90^{\circ}+\angle BCA+\angle FBD$,又因为$\angle FBD=\angle CAD$,$\angle BCA+\angle CAD = 90^{\circ}$,所以$\angle BCG+\angle FBD = 180^{\circ}-\angle BEC=90^{\circ}$($\angle BEC = 90^{\circ}$),$\angle BCG = 90^{\circ}+\angle BCA$,$\angle FBD+\angle BCA = 90^{\circ}$,所以$\angle FBC+\angle BCG=90^{\circ}$($\angle FBC=\angle FBD$),$\angle BCG = 90^{\circ}+\angle BCA$,$\angle FBC+\angle BCA = 90^{\circ}$,$\angle FBC+\angle BCG=\angle FBC + 90^{\circ}+\angle BCA=180^{\circ}$,$\angle BCG-\angle BCA = 90^{\circ}$,$\angle FBC=\angle BCA$(由$\triangle BDF\cong\triangle ADC$)不成立,重新分析:
因为$\angle ACG = 90^{\circ}$,$\angle BCD$为锐角,$\angle BCG=\angle BCD + 90^{\circ}$,$\triangle BDF\cong\triangle ADC$,$BF = AC$,$AC = GC$,所以$BF = GC$。
过$G$作$GH\perp BC$交$BC$延长线于$H$。
因为$\angle ACG = 90^{\circ}$,$\angle ADC = 90^{\circ}$,$\angle ACD+\angle HCG=90^{\circ}$,$\angle ACD+\angle CAD = 90^{\circ}$,所以$\angle CAD=\angle HCG$。
又$AC = GC$,$\angle ADC=\angle H = 90^{\circ}$,所以$\triangle ADC\cong\triangle CHG(AAS)$。
则$CH = AD = 2$,$GH = CD = 1$。
$BH=BC + CH=3 + 2=5$。
在$Rt\triangle BGH$中,根据勾股定理$BG=\sqrt{BH^{2}+GH^{2}}$。
把$BH = 5$,$GH = 1$代入可得$BG=\sqrt{5^{2}+1^{2}}=\sqrt{25 + 1}=\sqrt{26}$。
综上,(1)得证$BF = AC$;(2)$BG$的长为$\sqrt{26}$。
10. 如图,在$\triangle ABC$中,$\angle CAB = 20^{\circ}$,$\angle ABC = 30^{\circ}$,将$\triangle ABC$绕点$A$逆时针旋转$50^{\circ}$得到$\triangle AB'C'$,连接$CC'$,$BB'$。有以下结论:①$BC = B'C'$;②$AC// C'B'$;③$C'B'\perp BB'$;④$\angle ABB'=\angle ACC'$。其中正确的有(
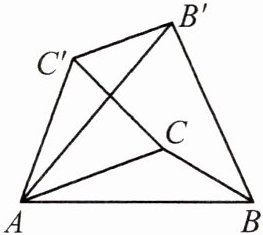
A. ①②③
B. ①②④
C. ①③④
D. ②③④
B
)
A. ①②③
B. ①②④
C. ①③④
D. ②③④
答案:
B
11. (2024·大庆改编)如图,在矩形$ABCD$中,$AB = 10$,$BC = 6$,$M$是$AB$边的中点,$N$是$AD$边上任意一点,将线段$MN$绕点$M$顺时针旋转$90^{\circ}$,点$N$旋转到点$N'$,则$\triangle MBN'$的周长的最小值为
$5 + 5\sqrt{5}$
。
答案:
$5 + 5\sqrt{5}$
12. (2024·北京)已知$\angle MAN=\alpha(0^{\circ}<\alpha<45^{\circ})$,点$B$,$C$分别在射线$AN$,$AM$上,将线段$BC$绕点$B$顺时针旋转$180^{\circ}-2\alpha$得到线段$BD$,过点$D$作$AN$的垂线交射线$AM$于点$E$。
(1)如图1,当点$D$在射线$AN$上时,求证:$C$是$AE$的中点;
(2)如图2,当点$D$在$\angle MAN$内部时,作$DF// AN$,交射线$AM$于点$F$,用等式表示线段$EF$与$AC$之间的数量关系,并证明。
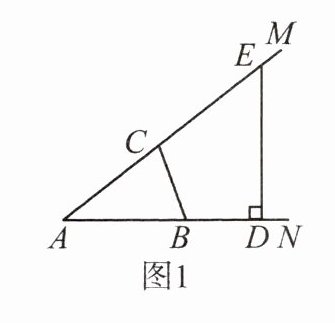

(1)如图1,当点$D$在射线$AN$上时,求证:$C$是$AE$的中点;
(2)如图2,当点$D$在$\angle MAN$内部时,作$DF// AN$,交射线$AM$于点$F$,用等式表示线段$EF$与$AC$之间的数量关系,并证明。


答案:
$(1)$ 证明$C$是$AE$的中点
解(证明):
已知线段$BC$绕点$B$顺时针旋转$180^{\circ}-2\alpha$得到线段$BD$,当点$D$在射线$AN$上时,$\angle CBD = 180^{\circ}-2\alpha$,$\angle MAN=\alpha$。
因为$\angle ACB$是$\triangle BCD$的外角,所以$\angle ACB=\angle CDB+\angle CBD\div2$(等腰三角形性质,$BC = BD$),$\angle CDB=\angle ACB-\alpha$。
又因为$ED\perp AN$,$\angle A = \alpha$,$\angle EDA = 90^{\circ}$,所以$\angle AED=90^{\circ}-\alpha$。
在$\triangle ABC$中,$\angle ABC = 180^{\circ}-\alpha-\angle ACB$,$\angle EBD = 180^{\circ}-\angle CBD-\angle ABC= \alpha$,则$\angle E = \angle ECB$(等角对等边),所以$AC = CE$,即$C$是$AE$的中点。
$(2)$ 求线段$EF$与$AC$之间的数量关系并证明
解(证明):
数量关系为$EF = 2AC$。
过点$B$作$BG\perp AM$于点$G$。
因为$DF// AN$,所以$\angle AFD+\angle A=180^{\circ}$,$\angle A=\alpha$,则$\angle AFD = 180^{\circ}-\alpha$。
由旋转知$BC = BD$,$\angle CBD=180^{\circ}-2\alpha$,所以$\angle BCD=\angle BDC=\alpha$。
因为$DF// AN$,所以$\angle FDB=\angle DBN$,$\angle A=\alpha$,$\angle ABG = 90^{\circ}-\alpha$。
又因为$ED\perp AN$,$BG\perp AM$,可证$\triangle BCG\cong\triangle BDF$($AAS$或$ASA$,根据角的关系和$BC = BD$)。
由$(1)$中思路可推得$AC = CF$(通过证明三角形中的角相等,得到边相等关系),所以$EF=EC + CF$,又因为$AC = CE$(类似$(1)$中证明$\angle E=\angle ECA$),所以$EF = 2AC$ 。
综上,$(1)$得证$C$是$AE$中点;$(2)$线段$EF$与$AC$的数量关系为$\boldsymbol{EF = 2AC}$。
解(证明):
已知线段$BC$绕点$B$顺时针旋转$180^{\circ}-2\alpha$得到线段$BD$,当点$D$在射线$AN$上时,$\angle CBD = 180^{\circ}-2\alpha$,$\angle MAN=\alpha$。
因为$\angle ACB$是$\triangle BCD$的外角,所以$\angle ACB=\angle CDB+\angle CBD\div2$(等腰三角形性质,$BC = BD$),$\angle CDB=\angle ACB-\alpha$。
又因为$ED\perp AN$,$\angle A = \alpha$,$\angle EDA = 90^{\circ}$,所以$\angle AED=90^{\circ}-\alpha$。
在$\triangle ABC$中,$\angle ABC = 180^{\circ}-\alpha-\angle ACB$,$\angle EBD = 180^{\circ}-\angle CBD-\angle ABC= \alpha$,则$\angle E = \angle ECB$(等角对等边),所以$AC = CE$,即$C$是$AE$的中点。
$(2)$ 求线段$EF$与$AC$之间的数量关系并证明
解(证明):
数量关系为$EF = 2AC$。
过点$B$作$BG\perp AM$于点$G$。
因为$DF// AN$,所以$\angle AFD+\angle A=180^{\circ}$,$\angle A=\alpha$,则$\angle AFD = 180^{\circ}-\alpha$。
由旋转知$BC = BD$,$\angle CBD=180^{\circ}-2\alpha$,所以$\angle BCD=\angle BDC=\alpha$。
因为$DF// AN$,所以$\angle FDB=\angle DBN$,$\angle A=\alpha$,$\angle ABG = 90^{\circ}-\alpha$。
又因为$ED\perp AN$,$BG\perp AM$,可证$\triangle BCG\cong\triangle BDF$($AAS$或$ASA$,根据角的关系和$BC = BD$)。
由$(1)$中思路可推得$AC = CF$(通过证明三角形中的角相等,得到边相等关系),所以$EF=EC + CF$,又因为$AC = CE$(类似$(1)$中证明$\angle E=\angle ECA$),所以$EF = 2AC$ 。
综上,$(1)$得证$C$是$AE$中点;$(2)$线段$EF$与$AC$的数量关系为$\boldsymbol{EF = 2AC}$。
查看更多完整答案,请扫码查看


