第94页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
1. 如图,AD 为$\odot O$的直径,$\overset{\frown}{AB}=\overset{\frown}{CD}$。若$∠AOB=45^{\circ }$,则$∠BOC=$(
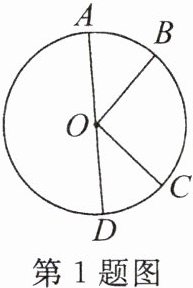
A.$30^{\circ }$
B.$45^{\circ }$
C.$60^{\circ }$
D.$90^{\circ }$
D
)
A.$30^{\circ }$
B.$45^{\circ }$
C.$60^{\circ }$
D.$90^{\circ }$
答案:
D
2. 如图,在$\odot O$中,C 是$\overset{\frown}{AB}$上的一点,且$\overset{\frown}{BC}=2\overset{\frown}{AC}$。若$∠A=36^{\circ }$,则$∠BOC$的度数是(
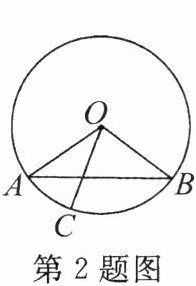
A.$72^{\circ }$
B.$70^{\circ }$
C.$68^{\circ }$
D.$66^{\circ }$
A
)
A.$72^{\circ }$
B.$70^{\circ }$
C.$68^{\circ }$
D.$66^{\circ }$
答案:
A
3. (易错)下列语句中,正确的有(
①相等的圆心角所对的弧相等;
②平分弦的直径垂直于弦;
③长度相等的两条弧是等弧;
④圆是轴对称图形,任何一条直径都是它的对称轴。
A. 3 个
B. 2 个
C. 1 个
D. 0 个
D
)①相等的圆心角所对的弧相等;
②平分弦的直径垂直于弦;
③长度相等的两条弧是等弧;
④圆是轴对称图形,任何一条直径都是它的对称轴。
A. 3 个
B. 2 个
C. 1 个
D. 0 个
答案:
D
4. (易错)计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比,同一个任务进行到不同阶段时,进度条的示意图如图所示,当任务完成的百分比为 x 时,线段 MN 的长度记为$d(x)$。下列描述正确的是(

A. 当$x_{1}\lt x_{2}$时,$d(x_{1})\lt d(x_{2})$
B. 当$d(x_{1})\lt d(x_{2})$时,$x_{1}\lt x_{2}$
C. 当$x_{1}=2x_{2}$时,$d(x_{1})=2d(x_{2})$
D. 当$x_{1}+x_{2}=1$时,$d(x_{1})=d(x_{2})$
D
)
A. 当$x_{1}\lt x_{2}$时,$d(x_{1})\lt d(x_{2})$
B. 当$d(x_{1})\lt d(x_{2})$时,$x_{1}\lt x_{2}$
C. 当$x_{1}=2x_{2}$时,$d(x_{1})=2d(x_{2})$
D. 当$x_{1}+x_{2}=1$时,$d(x_{1})=d(x_{2})$
答案:
D
5. (教材 P85 练习 T1 变式)如图,点 A,B,C 在$\odot O$上,连接 OA,OB,OC。
(1)若$∠AOB=∠AOC$,则$\overset{\frown}{AB}=$
(2)若$AC=BC$,则$\overset{\frown}{AC}=$
(3)若$\overset{\frown}{AB}=\overset{\frown}{BC}$,则$AB=$
(4)若$\triangle ABC$是等边三角形,则$∠BOC$的度数是
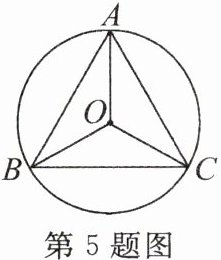
(1)若$∠AOB=∠AOC$,则$\overset{\frown}{AB}=$
$\overset{\frown}{AC}$
,$AB=$AC
;(2)若$AC=BC$,则$\overset{\frown}{AC}=$
$\overset{\frown}{BC}$
,$∠AOC=$$\angle BOC$
;(3)若$\overset{\frown}{AB}=\overset{\frown}{BC}$,则$AB=$
BC
,$∠AOB=$$\angle BOC$
;(4)若$\triangle ABC$是等边三角形,则$∠BOC$的度数是
$120^{\circ}$
。
答案:
(1)$\overset{\frown}{AC}$ AC
(2)$\overset{\frown}{BC}$ $\angle BOC$
(3)BC $\angle BOC$
(4)$120^{\circ}$
(1)$\overset{\frown}{AC}$ AC
(2)$\overset{\frown}{BC}$ $\angle BOC$
(3)BC $\angle BOC$
(4)$120^{\circ}$
6. (教材 P85 练习 T2 变式)如图,AB 是$\odot O$的直径,$\overset{\frown}{BC}=\overset{\frown}{CD}=\overset{\frown}{DE}$,$∠COD=32^{\circ }$,则$∠AEO$的度数是

48°
。
答案:
48°
7. 如图,已知 A,B 是$\odot O$上的点,$∠AOB=120^{\circ }$,C 是$\overset{\frown}{AB}$的中点。若$\odot O$的半径为 2,则四边形 ACBO 的面积为
$2\sqrt{3}$
。
答案:
$2\sqrt{3}$
8. (教材 P85 练习 T1(4)变式)如图,在$\odot O$中,A,B,C,D 是圆上的四点,且$AB=CD$,过圆心 O 作$OE⊥AB$,垂足为 E。
(1)用直尺和圆规,过点 O 作$OF⊥CD$,垂足为 F(只保留作图痕迹,不写过程);
(2)在(1)的条件下,求证:$OE=OF$;
(3)依照题意完成下面的命题:在同圆或等圆中,若两弦相等,则

(1)用直尺和圆规,过点 O 作$OF⊥CD$,垂足为 F(只保留作图痕迹,不写过程);
(2)在(1)的条件下,求证:$OE=OF$;
(3)依照题意完成下面的命题:在同圆或等圆中,若两弦相等,则
圆心到这两条弦的距离相等
。
答案:
(1)略
(2)略
(3)圆心到这两条弦的距离相等
(1)略
(2)略
(3)圆心到这两条弦的距离相等
查看更多完整答案,请扫码查看


