《2025年一本同步训练九年级数学上册人教版重庆专版》

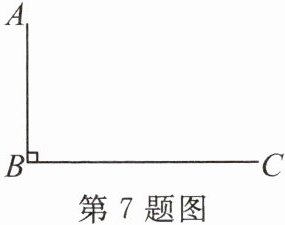
7. 如图，在马拉松比赛过程中，中间的某段路径为$A - B - C$.在比赛期间，小琪和小明之间一直用最远对讲距离为300m的对讲设备保持联系.小琪运动到A点时，用对讲机联系小明，小明告知小琪他正在通过路口B并向点C运动后，就失去了联系.已知小琪的跑步速度为2m/s，小明的跑步速度为4m/s，$\angle ABC = 90^{\circ}$，BC足够长，则多久后他们可以再次取得联系（B）

A. 150s
B. 60s
C. 100s
D. 不会再取得联系

答案： B

8. 如图，将矩形沿虚线剪成四部分，用这四部分恰能拼一个正方形.若$x = 1$，则$y =$$\frac{-1+\sqrt{5}}{2}$.

答案： $\frac{-1+\sqrt{5}}{2}$

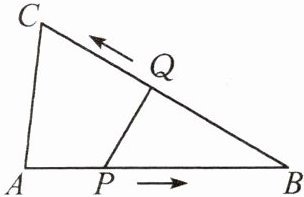
9. 如图，在$\triangle ABC$中，$AB = 6cm$，$BC = 7cm$，$\angle ABC = 30^{\circ}$，点P从A点出发，以1cm/s的速度向B点移动，点Q从B点出发，以2cm/s的速度向C点移动，当一个点到达终点时，另一个点也随即停止运动.已知P，Q两点同时出发，设运动时间为t s.
(1)经过几秒后，$\triangle PBQ$的面积等于4cm²？
(2)四边形APQC的面积能否等于5.5cm²？请说明理由.

答案： 1. （1）
首先，根据已知条件表示出$BP$和$BQ$的长度：
已知$AP = t$，$BQ = 2t$，则$BP=(6 - t)$。
根据三角形面积公式$S=\frac{1}{2}ab\sin C$（这里$a = BP$，$b = BQ$，$C=\angle ABC = 30^{\circ}$），$\triangle PBQ$的面积$S_{\triangle PBQ}=\frac{1}{2}BP\cdot BQ\cdot\sin\angle ABC$。
因为$\sin30^{\circ}=\frac{1}{2}$，所以$S_{\triangle PBQ}=\frac{1}{2}(6 - t)\times2t\times\frac{1}{2}$。
然后，令$S_{\triangle PBQ}=4$：
则$\frac{1}{2}(6 - t)\times2t\times\frac{1}{2}=4$。
化简得$(6 - t)t = 8$。
展开式子得$6t-t^{2}=8$。
移项化为一元二次方程的标准形式$t^{2}-6t + 8 = 0$。
分解因式得$(t - 2)(t - 4)=0$。
解得$t_{1}=2$，$t_{2}=4$。
又因为$0\leqslant t\leqslant3.5$（当$Q$到达终点时，$t=\frac{7}{2}=3.5$），所以$t = 2$。
2. （2）
先求$\triangle ABC$的面积：
根据三角形面积公式$S_{\triangle ABC}=\frac{1}{2}AB\cdot BC\cdot\sin\angle ABC$。
已知$AB = 6$，$BC = 7$，$\sin30^{\circ}=\frac{1}{2}$，则$S_{\triangle ABC}=\frac{1}{2}\times6\times7\times\frac{1}{2}=\frac{21}{2}$。
再求$S_{\triangle PBQ}$：
若$S_{四边形APQC}=5.5$，因为$S_{四边形APQC}=S_{\triangle ABC}-S_{\triangle PBQ}$，则$S_{\triangle PBQ}=S_{\triangle ABC}-S_{四边形APQC}$。
把$S_{\triangle ABC}=\frac{21}{2}$，$S_{四边形APQC}=5.5$代入得$S_{\triangle PBQ}=\frac{21}{2}-5.5=\frac{21 - 11}{2}=5$。
由$S_{\triangle PBQ}=\frac{1}{2}(6 - t)\times2t\times\frac{1}{2}=5$。
化简得$(6 - t)t = 10$。
即$t^{2}-6t + 10 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0$（这里$a = 1$，$b=-6$，$c = 10$），判别式$\Delta=b^{2}-4ac=(-6)^{2}-4\times1\times10=36 - 40=-4\lt0$。
所以方程$t^{2}-6t + 10 = 0$无实数根，即四边形$APQC$的面积不能等于$5.5cm^{2}$。
综上，（1）经过$2s$后，$\triangle PBQ$的面积等于$4cm^{2}$；（2）四边形$APQC$的面积不能等于$5.5cm^{2}$。

10. 【综合与实践】
九年级课外小组计划用两块长为100cm、宽为40cm的长方形硬纸板做收纳盒.
善思组：如图1，把一块长方形硬纸板的四角剪去四个相同的小正方形，然后沿虚线折成一个无盖的长方体收纳盒.
问题解决：(1)若该收纳盒的底面积为1600cm²，设剪去的小正方形的边长为x cm，则可列方程为(100 - 2x)(40 - 2x)=1600，求得剪去的小正方形的边长为10cm.
博学组：如图2，把另一块长方形硬纸板的四角剪去四个相同的小长方形，然后沿虚线折成一个有盖的长方体收纳盒.
问题解决：(2)若EF和HG两边恰好重合且无重叠部分，该收纳盒的底面积为608cm²，设收纳盒的高为a cm，则收纳盒底面的长为(100 - 2a)cm，宽为(20 - a)cm(用含a的代数式表示)，则可列方程为(100 - 2a)(20 - a)=608.若有一个玩具机械狗，其尺寸大小如图3所示，请判断是否能把该玩具机械狗完全立着放入该收纳盒，并说明理由.
问题解决：(3)按照博学组的剪法，可以(填“可以”或“不可以”)剪出一个收纳盒把玩具机械狗完全放入(立放或者平放).

答案：
(1)$(100 - 2x)(40 - 2x)=1600$；$10$。
(2)$(100 - 2a)$；$(20 - a)$；$(100 - 2a)(20 - a)=608$。
(3)可以。